题目内容
(本小题满分10分)
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M, AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,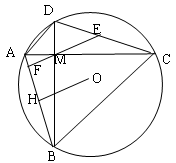
求证:(1)EF⊥AB (2)OH=ME
(1)根据对顶角,和同弧所对的圆周角相等来证明。
(2)根据平行四边形的性质来证明角相等。
解析试题分析:(1)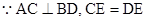


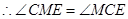
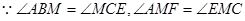
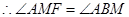
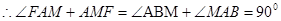
 ……………………………………………………………………5分
……………………………………………………………………5分
(2)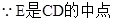

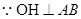
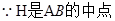
连结HM,并延长交CD于G,又(1)的证法,可证
∴OE∥HG ,OH∥EF
∴OEMH是平行四边形
∴OH=ME…………………………………………………………………10分
考点:本试题考查了平面几何的运用。
点评:对于平面几何中的线段的相等,一般通过证明角相等来得到边相等。同时垂直的证明,只要证明三角形中其余的两个角和为直角即可。属于基础题。

练习册系列答案
相关题目
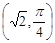 ,直线
,直线 的极坐标方程为
的极坐标方程为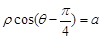 ,且点A在直线
,且点A在直线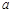 的值及直线
的值及直线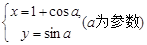 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.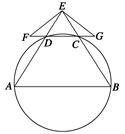
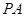 与圆
与圆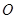 相切于点
相切于点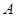 ,经过点
,经过点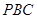 交圆
交圆 、
、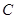 ,
,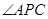 的平分线分别交
的平分线分别交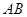 、
、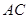 于点
于点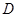 、
、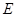 .
.
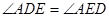 .
.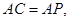 求
求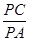 的值.
的值.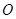 外一点
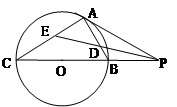
外一点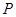 引圆的两条切线
引圆的两条切线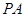 ,
, 及一条割线
及一条割线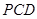 ,
,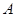 、
、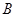 为切点.求证:
为切点.求证: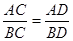
 中,∠
中,∠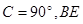 是角平分线,
是角平分线, 交
交 于
于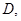 ⊙
⊙ 是△
是△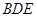 的外接圆。
的外接圆。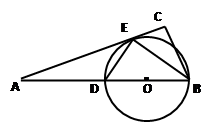
 是⊙
是⊙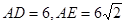 ,求
,求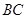 的长。
的长。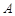 ,D为
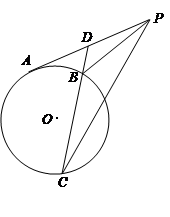
,D为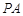 的中点,过点D引割线交⊙O于
的中点,过点D引割线交⊙O于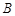 、
、 两点.
两点.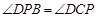 .
.
 中,
中,
 在线
在线 段
段 上,且
上,且 ,
,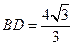
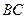 的长;
的长; 的面积.
的面积.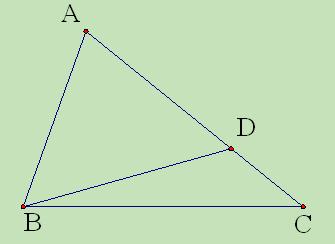
 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形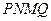 ,使点
,使点 在
在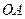 上,点
上,点 在
在 上,设矩形
上,设矩形 ,
,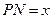 ,将
,将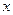 的函数关系式;
的函数关系式; ,将
,将