题目内容

半径为10cm的球被两个平行平面所截，两个截面圆的面积分别为36πcm2，64πcm2，求这两个平行平面的距离．

设两个截面圆的半径别为r1，r2．球心到截面的距离分别为d1，d2．
球的半径为R．
由πr12=36πcm2，得r1=6cm．
由πr22=64πcm2，得r2=8cm．
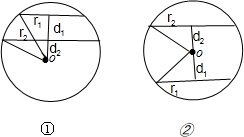
如图①所示．当球的球心在两个平行平面的外侧时，
这两个平面间的距离为球心与两个截面圆的距离之差．
即d2-d1=
R2-r12
-
R2-r22
=
102-36
-
102-82
=8-6=2cm．
如图②所示．当球的球心在两个平行平面的之间时，
这两个平面间的距离为球心与两个截面圆的距离之和．
即d2+d1=
R2-r12
+
R2-r22
=8+6=14cm．
练习册系列答案
相关题目
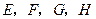已知分别是空间四边形的边上的点，
且四边形是平行四边形，求证：平面，平面．
 
如图，ABCD是菱形，PA⊥平面ABCD，PA=AD=2，∠BAD=60，
（1）求点A到平面PBD的距离的值；
（2）求二面角A-PB-D的余弦值．
三棱锥P-ABC的三条侧棱两两垂直，Q为底面上一点，Q到三个侧面的距离分别为3、4、5，则PQ的长度为（　　）
A．5B．5
2
C．4
2
D．6
（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（1）求异面直线EG与BD所成角的大小；
（2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为
4
5
？若存在，求出线段CQ的长；若不存在，请说明理由．
已知P是边长为a的正六边形ABCDEF所成平面外一点，PA⊥AB，PA⊥AF，PA=a．则点P到边CD的距离是______．
如图，在四棱锥M-ABCD中，底面ABCD是边长为2的正方形，侧棱AM的长为3，且AM和AB、AD的夹角都是60°，N是CM的中点，设
a
=
AB
，
b
=
AD
，
c
=A
M
，试以
a
，
b
，
c
为基向量表示出向量
BN
，并求BN的长．
已知直二面角α-l-β，A∈α，B∈β，A，B两点均不在直线l上，又直线AB与l成30°角，且线段AB=8，则线段AB的中点M到l的距离为______．
棱长为a的正方体A1B1C1D1-ABCD中，O为面ABCD的中心．
（1）求证：AC1⊥平面B1CD1；
（2）求四面体OBC1D1的体积；
（3）线段AC上是否存在P点（不与A点重合），使得A1P∥面CC1D1D？如果存在，请确定P点位置，如果不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网