题目内容
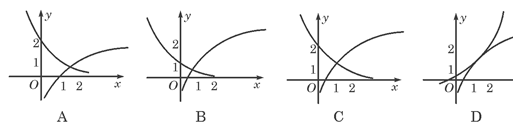
函数f(x)=1+log2x与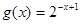 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )
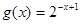 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )
C
根据函数f(x)=1+log2x与g(x)=2-x+1解析式,分析他们与同底的指数函数、对数函数的图象之间的关系,(即如何变换得到),分析其经过的特殊点,即可用排除法得到答案.
解:∵f(x)=1+log2x的图象是由y=log2x的图象上移1而得,
∴其图象必过点(1,1).
故排除A、B,
又∵g(x)=2-x+1=2-(x-1)的图象是由y=2-x的图象右移1而得
故其图象也必过(1,1)点,及(0,2)点,
故排除D
故选C
解:∵f(x)=1+log2x的图象是由y=log2x的图象上移1而得,
∴其图象必过点(1,1).
故排除A、B,
又∵g(x)=2-x+1=2-(x-1)的图象是由y=2-x的图象右移1而得
故其图象也必过(1,1)点,及(0,2)点,
故排除D
故选C

练习册系列答案
相关题目
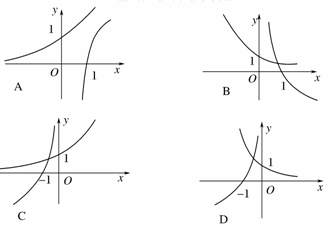
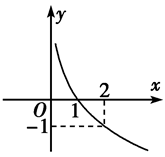
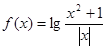 (
(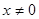 ,
,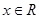 ), 有下列命题:
), 有下列命题: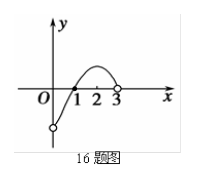
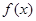 的图象关于y轴对称;
的图象关于y轴对称;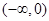 上是减函数,在
上是减函数,在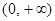 上是增函数;
上是增函数;

 ,则函数
,则函数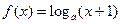 的图像大致是
的图像大致是 
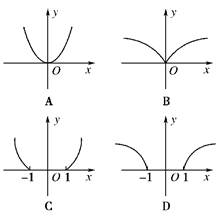
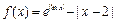 的图象为( )
的图象为( )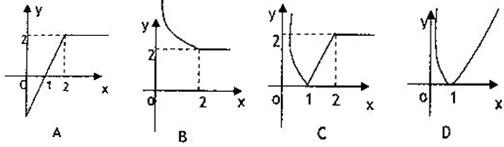
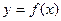 的那一个图是
的那一个图是