题目内容
(Ⅰ)设a1,a2,a3均为正数,且a1+a2+a3=m,求证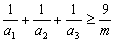 ;
;
(Ⅱ)已知a,b都是正数,x,y∈R,且a+b=1,求证:ax2+by2≥(ax+by)2。
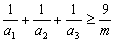 ;
;(Ⅱ)已知a,b都是正数,x,y∈R,且a+b=1,求证:ax2+by2≥(ax+by)2。
证明:(Ⅰ)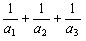
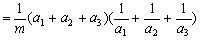
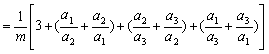
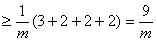 ,
,
当且仅当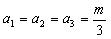 时,等号成立;
时,等号成立;
(Ⅱ)ax2+by2=(ax2+by2)(a+b)=a2x2+b2y2+ab(x2+y2)≥a2x2+b2y2+2abxy=(ax+by)2。
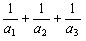
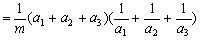
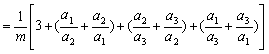
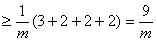 ,
,当且仅当
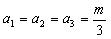 时,等号成立;
时,等号成立;(Ⅱ)ax2+by2=(ax2+by2)(a+b)=a2x2+b2y2+ab(x2+y2)≥a2x2+b2y2+2abxy=(ax+by)2。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目