题目内容
0.3| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:函数f(x)=x
在[0,+∞)上是递增函数,0.3<2.1<2.2,所以0.3
<2.1
<2.2
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵函数f(x)=x
在[0,+∞)上是递增函数,
∴f(0.3)<f(2.1)<f(2.2),
即:0.3
<2.1
<2.2
.
答案:0.3
<2.1
<2.2
.
| 1 |
| 2 |
∴f(0.3)<f(2.1)<f(2.2),
即:0.3
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答案:0.3
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查幂函数的性质和应用,解题时要注意f(x)=x
在[0,+∞)上是递增函数,合理地运用函数的单调性.
| 1 |
| 2 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
某校从甲、乙两名优秀选手中选拔1名参加全市中学生百米比赛,该校预先对这两名选手测试了8次,成绩如下表:
选手成绩(s) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
甲 | 12.1 | 12.2 | 13 | 12.5 | 13.1 | 12.5 | 12.4 | 12.2 |
乙 | 12 | 12.4 | 12.8 | 13 | 12.2 | 12.8 | 12.3 | 12.5 |
根据成绩,请你作出判断,派哪位选手参加更好,为什么?
 (2005年上海高考题)用n个不同的实数a1,a2,…,an可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3,…,n!.用1,2,3可得数阵如右,由于此数阵中每一列各数之和都是12,所以,b1+b2+┄+b6=-12+2
(2005年上海高考题)用n个不同的实数a1,a2,…,an可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3,…,n!.用1,2,3可得数阵如右,由于此数阵中每一列各数之和都是12,所以,b1+b2+┄+b6=-12+2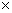 12-3
12-3