题目内容
1.已知抛物线y2=2px(p>0)的焦点F到其准线的距离是2,那么p等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求得抛物线y2=2px(p>0)的焦点为($\frac{p}{2}$,0),准线为x=-$\frac{p}{2}$,则焦点到准线的距离为p,由题意即可得到p的值.
解答 解:抛物线y2=2px(p>0)的焦点为($\frac{p}{2}$,0),
准线为x=-$\frac{p}{2}$,
则焦点到准线的距离为p,
由题意可得p=2.
故选B.
点评 本题考查抛物线的方程和性质,主要考查抛物线的焦点和准线方程,同时考查点到直线的距离,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
13. 如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
 如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )| A. | y2=20x | B. | y2=10x | C. | y2=5x | D. | y2=$\frac{5}{2}$x |
10.已知全集U={1,2,3,4,5},集合M={3,4,5},N={1,2,5},则集合{1,2}可以表示为( )
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∩(∁UN) |
11. 一个体积为$\frac{25}{3}$的四棱锥的主视图和俯视图如图所示,则该棱锥的左视图的面积为( )
一个体积为$\frac{25}{3}$的四棱锥的主视图和俯视图如图所示,则该棱锥的左视图的面积为( )
 一个体积为$\frac{25}{3}$的四棱锥的主视图和俯视图如图所示,则该棱锥的左视图的面积为( )
一个体积为$\frac{25}{3}$的四棱锥的主视图和俯视图如图所示,则该棱锥的左视图的面积为( )| A. | $\frac{25}{2}$ | B. | $\frac{25}{3}$ | C. | $\frac{25}{4}$ | D. | $\frac{25}{6}$ |
 若
若 ,则实数
,则实数 等于( )
等于( )

 ,
, ,函数
,函数 若
若 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 是
是 的重心,过点
的重心,过点 作直线与
作直线与 两边分别交于
两边分别交于 两点,且
两点,且 ,则
,则 的最小值为( )
的最小值为( )
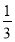
 D.
D.
 为平面向量,若
为平面向量,若 与
与 的夹角为
的夹角为 与
与 的夹角为
的夹角为 ,则
,则 ( )
( ) B.
B.
 D.2
D.2