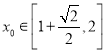题目内容
【题目】设函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() ,
,![]() ,证明
,证明![]() ;
;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有两个零点?若存在,求出
上有两个零点?若存在,求出![]() 的取值范围:若不存在,请说明理由.
的取值范围:若不存在,请说明理由.
【答案】(1)证明见解析(2)不存在实数![]() ,详见解析
,详见解析
【解析】
(1)分类讨论,![]() 时直接证明,
时直接证明,![]() 时,利用导数研究函数的单调性,最小值可证得不等式成立;
时,利用导数研究函数的单调性,最小值可证得不等式成立;
(2)![]() 时,由(1)可知无零点,
时,由(1)可知无零点,![]() 时,仍然利用导数研究函数的单调性,函数极值,结合零点存在定理确定零点个数.
时,仍然利用导数研究函数的单调性,函数极值,结合零点存在定理确定零点个数.
(1)证明:①若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ;
;
②若![]() ,因为
,因为![]() ,
,
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
综上所述,若![]() ,
,![]() ,则
,则![]() .
.
(2)不存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.
理由如下:
(1)若![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上无零点;
上无零点;
(2)若![]() ,由(1)知,当
,由(1)知,当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增.因为
上单调递增.因为![]() ,
,![]() ,
,
所以![]() 在
在![]() 上存在唯一的零点
上存在唯一的零点![]() ,
,
即方程![]() 在
在![]() 上存在唯一解
上存在唯一解![]() ,
,
且当![]() 时,
时,![]() ,当
,当![]() ,
,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 无零点;
无零点;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一零点,
上有唯一零点,
故当![]() 时,
时,![]() 在
在![]() 上有一个零点,
上有一个零点,
综上所述,不存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.

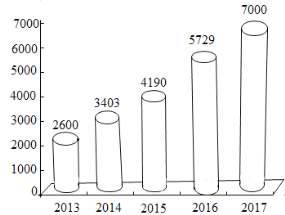
【题目】网购已经成为一种新型的购物方式,2018年天猫双11,仅1小时47分钟成交额超过1000亿元,比2017年达到1000亿元的时间缩短了7个小时,为了研究市民对网购的依赖性,从A城市16﹣59岁人群中抽取一个容量为100的样本,得出下列2×2列联表,其中16﹣39岁为青年,40﹣59岁为中年,当日消费金额超过1000元为消费依赖网购,否则为消费不依赖网购.
依赖网购 | 不依赖网购 | 小计 | |
青年(16﹣39岁) | 40 | 20 | |
中年(40﹣59岁) | 20 | 20 | |
小计 |
(1)完成2×2列联表,计算X2值,并判断是否有95%的把握认为网购依赖和年龄有关?
(2)把样本中的频率当作概率,随机从A城市中选取5人,其中依赖网购的人数为随机变量X,求随机变量X的分布列及期望(附:X2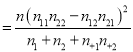 ,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)