题目内容
（2010•武清区一模）已知函数f（x）是定义在R上的偶函数，则“f（x）是周期函数”的一个充要条件是（ ）
分析：根据充要条件的定义，逐一判断四个答案中的条件，与“f（x）是周期函数”的充要关系，比照后即可得到答案．
解答：解：f（x）=cosx，则函数的周期为2π，故“f（x）=cosx”是“f（x）是周期函数”的一个充分不必要条件，故A不正确；
?α∈R，f（α+x）=f（α-x），则任意实数都是函数的周期，故“?α∈R，f（α+x）=f（α-x）”是“f（x）是周期函数”的一个充分不必要条件，故B不正确；
f（1+x）=f（1-x），则函数的周期为2，故“f（1+x）=f（1-x）”是“f（x）是周期函数”的一个充分不必要条件，故C不正确；
?α∈R（α≠0），f（α+x）=f（α-x），则函数的周期为2α，故“?α∈R（α≠0），f（α+x）=f（α-x）”是“f（x）是周期函数”的一个充分不必要条件，故D正确；
故选D
?α∈R，f（α+x）=f（α-x），则任意实数都是函数的周期，故“?α∈R，f（α+x）=f（α-x）”是“f（x）是周期函数”的一个充分不必要条件，故B不正确；
f（1+x）=f（1-x），则函数的周期为2，故“f（1+x）=f（1-x）”是“f（x）是周期函数”的一个充分不必要条件，故C不正确；
?α∈R（α≠0），f（α+x）=f（α-x），则函数的周期为2α，故“?α∈R（α≠0），f（α+x）=f（α-x）”是“f（x）是周期函数”的一个充分不必要条件，故D正确；
故选D
点评：本题考查的知识点是必要条件、充分条件与充要条件的判断，函数的周期性，其中熟练掌握函数奇偶性，对称性，是解答本题的关键．
练习册系列答案
口算能手系列答案
相关题目
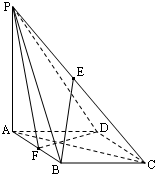（2010•武清区一模）如图所示，在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°AB=PA=2，PA⊥平面ABCD，E是PC的中点，F是AB的中点．