题目内容
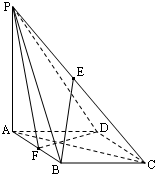 (2010•武清区一模)如图所示,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(2010•武清区一模)如图所示,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求BE与平面PAC所成的角.
分析:(1)利用线面平行的判定定理去证明.(2)利用面面垂直的判定定理去证明.(3)利用定义或向量法求直线与平面所成的角.
解答: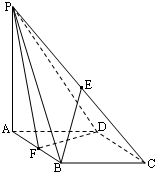 解:(1)证明:取PD的中点为M,连接ME,MF,
解:(1)证明:取PD的中点为M,连接ME,MF,
∵E是PC的中点,∴ME是△PCD的中位线.
∴ME∥CD,ME=
CD.
又∵F是AB的中点,且由于ABCD是菱形,
∴AB∥CD,AB=CD,∴ME∥FB,且ME=FB.
∴四边形MEBF是平行四边形,∴BE∥MF.
∵BE?平面PDF,MF?平面PDF,
∴BE∥平面PDF.
(2)证明:∵PA⊥平面ABCD,DF?平面ABCD,
∴DF⊥PA.连接BD,
∵底面ABCD是菱形,∠BAD=60°,∴△DAB为正三角形.
∵F是AB的中点,∴DF⊥AB.
∵PA∩AB=A,∴DF⊥平面PAB.
∵DF?平面PDF,∴平面PDF⊥平面PAB.
(3)连结BD交AC于O,∵底面ABCD是菱形,∴AC⊥BD,
∵PA⊥平面ABCD,∴PA⊥BD,∴BD⊥平面PAC.
∴OB⊥OE,即OE是BE在平面PAC上的射影.
∴∠BEO是BE与平面PAC所成的角.
∵O,E,分别是中点,∴OE=
AP=1,OD=
BD=
AB=1,
∴Rt△BOE为等腰直角三角形,∴∠BEO=45°,
即BE与平面PAC所成的角的大小为45°.
 解:(1)证明:取PD的中点为M,连接ME,MF,
解:(1)证明:取PD的中点为M,连接ME,MF,∵E是PC的中点,∴ME是△PCD的中位线.
∴ME∥CD,ME=
| 1 |
| 2 |
又∵F是AB的中点,且由于ABCD是菱形,
∴AB∥CD,AB=CD,∴ME∥FB,且ME=FB.
∴四边形MEBF是平行四边形,∴BE∥MF.
∵BE?平面PDF,MF?平面PDF,
∴BE∥平面PDF.
(2)证明:∵PA⊥平面ABCD,DF?平面ABCD,
∴DF⊥PA.连接BD,
∵底面ABCD是菱形,∠BAD=60°,∴△DAB为正三角形.
∵F是AB的中点,∴DF⊥AB.
∵PA∩AB=A,∴DF⊥平面PAB.
∵DF?平面PDF,∴平面PDF⊥平面PAB.
(3)连结BD交AC于O,∵底面ABCD是菱形,∴AC⊥BD,
∵PA⊥平面ABCD,∴PA⊥BD,∴BD⊥平面PAC.
∴OB⊥OE,即OE是BE在平面PAC上的射影.
∴∠BEO是BE与平面PAC所成的角.
∵O,E,分别是中点,∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Rt△BOE为等腰直角三角形,∴∠BEO=45°,
即BE与平面PAC所成的角的大小为45°.
点评:本题主要考查线面平行和面面垂直的位置关系的判定,要求熟练掌握线面、面面垂直与平行的判定定理和性质定理.综合性较强.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目