题目内容
 在直三棱柱ABC-A1B1C1中,A1A=AB=3
在直三棱柱ABC-A1B1C1中,A1A=AB=3| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
(1)求平面APQ与面ABC所成的锐二面角的大小.
(2)在线段A1B(不包括两端点)上是否存在一点M,使AM+MC1最小?若存在,求出最小值;若不存在,说明理由.
考点:二面角的平面角及求法,多面体和旋转体表面上的最短距离问题
专题:空间位置关系与距离
分析:(1)以A为原点建立空间直角坐标系A-xyz,利用向量法能求出平面APQ与面ABC所成的锐角大小.
(2)沿A1B将面A1BC1与面A1BA展开,连结AC1与A1B交于M,此时AM+MC1有最小值.由此能求出存在点M,使AM+AC1取最小值为3
.
(2)沿A1B将面A1BC1与面A1BA展开,连结AC1与A1B交于M,此时AM+MC1有最小值.由此能求出存在点M,使AM+AC1取最小值为3
| 5 |
解答:
解:(1)建立如图所示空间直角坐标系A-xyz,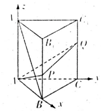
A(0,0,0),P(3
,0,
),Q(0,3,2
).
设平面APQ的一个法向量为
=(x,y,z),
,
令z=3,得
=(-1,-2
,3),
平面ABC的一个法向量
=(0,0,1),
∴cos<
,
>=
=
,
∴平面APQ与面ABC所成的锐角大小为45°.…(6分)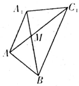
(2)沿A1B将面A1BC1与面A1BA展开,
连结AC1与A1B交于M,此时AM+MC1有最小值.
∵∠A1AB=90°,AA1=AB,∴∠A1AB=45°,
又C1A1⊥面ABB1A1,∴C1A1⊥A1B.
∴△AA1C1中,∠AA1C1=135°,
AC1=
=
=3
,
∴存在点M,使AM+AC1取最小值为3
.

A(0,0,0),P(3
| 2 |
| 2 |
| 2 |
设平面APQ的一个法向量为
| n1 |
|
令z=3,得
| n1 |
| 2 |
平面ABC的一个法向量
| n2 |
∴cos<
| n1 |
| n2 |
| 3 | ||
|
| ||
| 2 |
∴平面APQ与面ABC所成的锐角大小为45°.…(6分)

(2)沿A1B将面A1BC1与面A1BA展开,
连结AC1与A1B交于M,此时AM+MC1有最小值.
∵∠A1AB=90°,AA1=AB,∴∠A1AB=45°,
又C1A1⊥面ABB1A1,∴C1A1⊥A1B.
∴△AA1C1中,∠AA1C1=135°,
AC1=
| AA12+A1C12-2AA1•A1C1•cos135° |
=
| 18+9+18 |
| 5 |
∴存在点M,使AM+AC1取最小值为3
| 5 |
点评:本题考查平面APQ与面ABC所成的锐二面角的大小的求法,考查在线段A1B(不包括两端点)上是否存在一点M,使AM+MC1最小的判断与求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
下列函数是偶函数的是( )
| A、y=sinx |
| B、y=cosx |
| C、y=tanx |
| D、以上都不是 |
n个人随机进入n个房间,每个人可以进入任何一个房间,且进入各房间是等可能的,则每个房间恰好进入一个人的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知2
+
=(0,1),
=(1,-1),
•
=1,|
|=3,则
与
的夹角为 ( )
| a |
| b |
| c |
| a |
| c |
| b |
| b |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
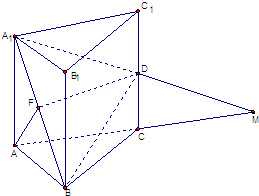 已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),
已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),