题目内容
16.已知定义在R上的函数f(x),对于任意实数x,y都满足f(x+y)=f(x)•f(y),且f(1)≠0,当x>0时,f(x)>1(1)求f(0)的值;
(2)证明f(x)在(-∞,+∞)上是增函数.
分析 (1)利用赋值法,即可求f(0)的值;
(2)利用函数单调性的定义,结合抽象函数的关系进行证明即可.
解答 (1)解:对于任意实数x,y都满足f(x+y)=f(x)•f(y),
令x=1,y=0,则f(1)=f(1)f(0),
∵f(1)≠0,∴f(0)=1.
(2)证明:当x<0,则-x>0,
则f(x)•f(-x)=f(x-x)=f(0)=1,
则f(-x)>0,则f(x)>0,
即f(x)>0恒成立
设x1,x2∈R,且x2<x1,则x1-x2>0,
∴f(x1-x2)=$\frac{f({x}_{1})}{f({x}_{2})}>1$,
∵对任意的x,y∈R,总有f(x)>0,
∴f(x1)>f(x2),
即f(x)在R上为增函数.
点评 本题主要考查函数单调性的判断以及函数最值的求解,根据抽象函数的关系,利用赋值法是解决抽象函数的基本方法,

练习册系列答案
相关题目
4.从我市某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,测量的原始数据已丢失,只余下频数分布表如下:
(Ⅰ)请你填写下面的频率分布表:若规定“质量指标值不低于30的产品为合格产品”,则该企业生的这种产品的合格率是多少?
(Ⅱ)请你估计这种产品质量指标值的众数、平均数、中位数的值(同一组中的数据用该组区间的中间值作代表).
| 质量指标值分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| 质量指标值分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 0.15 | 0.2 |
8.已知全集U=R,集合A={1,2,3,4,5},B={x∈R|x>2},下图中阴影部分所表示的集合为( )
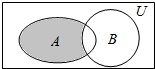

| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
5.下列函数中,既是偶函数,又在(0,+∞)单调递增的函数是( )
| A. | y=|lgx| | B. | y=2-|x| | C. | y=|$\frac{1}{x}$| | D. | y=lg|x| |
6.复数z=4i2016-$\frac{5i}{1+2i}$(其中i为虚数单位)对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
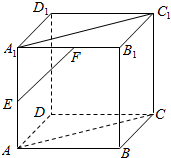 在正方体ABCD-A1B1C1D1中,E、F分别是A1A、A1B1的中点,求EF与平面A1ACC1所成的角.
在正方体ABCD-A1B1C1D1中,E、F分别是A1A、A1B1的中点,求EF与平面A1ACC1所成的角.