题目内容
如图,在正方体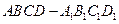 中,
中,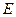 、
、 分别是棱
分别是棱 、
、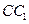 的中点.
的中点.
试画出平面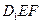 与平面
与平面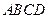 的交线.
的交线.
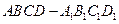 中,
中,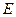 、
、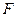 分别是棱
分别是棱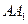 、
、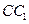 的中点.
的中点.试画出平面
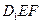 与平面
与平面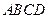 的交线.
的交线.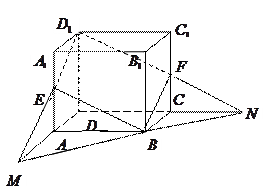 |
答案见解析
作法:平面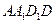 同时与平面
同时与平面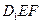 与平面
与平面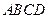 相交,其交线分别为
相交,其交线分别为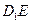 和
和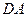 ,因此,分别延长
,因此,分别延长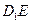 和
和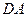 相交于点
相交于点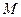 ,
,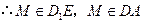 ,且
,且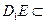 平面
平面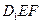 ,
,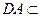 平面
平面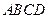 ,
,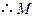 为平面
为平面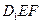 与平面
与平面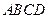 的一个公共点.同理可作出点
的一个公共点.同理可作出点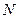 也是平面
也是平面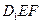 和平面
和平面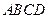 的公共点,连结
的公共点,连结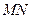 ,根据公理
,根据公理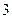 知,直线
知,直线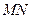 就是两个平面的交线.
就是两个平面的交线.
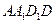 同时与平面
同时与平面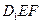 与平面
与平面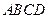 相交,其交线分别为
相交,其交线分别为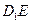 和
和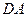 ,因此,分别延长
,因此,分别延长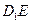 和
和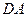 相交于点
相交于点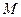 ,
,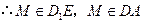 ,且
,且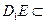 平面
平面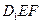 ,
,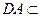 平面
平面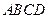 ,
,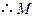 为平面
为平面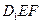 与平面
与平面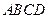 的一个公共点.同理可作出点
的一个公共点.同理可作出点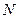 也是平面
也是平面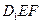 和平面
和平面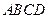 的公共点,连结
的公共点,连结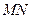 ,根据公理
,根据公理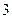 知,直线
知,直线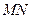 就是两个平面的交线.
就是两个平面的交线.
练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
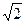 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面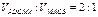 ;
;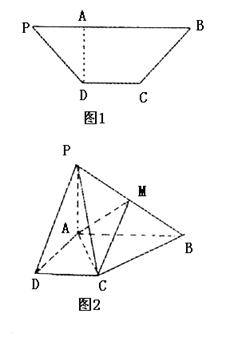
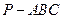 中,⊿
中,⊿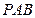 是等边三角形,∠PAC=∠PBC="90" º.
是等边三角形,∠PAC=∠PBC="90" º.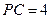 ,且平面
,且平面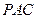 ⊥平面
⊥平面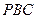 ,求三棱锥
,求三棱锥
 中,
中,  底面
底面 ,
,
 .
.
 分别为棱
分别为棱 的中点,求证:
的中点,求证: 平面
平面 ;
;
 (2)在四棱锥G—ABCD中,过点B作平面
(2)在四棱锥G—ABCD中,过点B作平面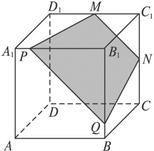
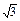 ,EF=2.
,EF=2.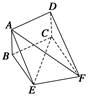
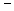 ABCD底面是直角梯形,
ABCD底面是直角梯形, 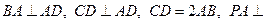 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1. 
 ;
; ;
;