题目内容
将三个小球随机地投入编号1,2,3,4的4个盒子中(每个盒子容纳的小球的个数没有限制),求:
(1)第1个盒子为空盒的概率;
(2)小球最多的盒子中小球的个数X的分布列和期望.
(1)第1个盒子为空盒的概率;
(2)小球最多的盒子中小球的个数X的分布列和期望.
(1)任意投放共有43=64(种)方法,若第1个盒子为空盒,则小球可随机地投入编号2,3,4的3个盒子中,有33=27(种)方法,故所求的概率为
.
(2)小球最多的盒子中小球的个数X的取值为1,2,3.则
P(X=1)=
=
;P(X=2)=
=
;P(X=3)=
=
.
故X的分布列为
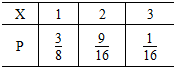
所以X的数学期望为E(X)=1×
+2×
+3×
=
.
| 27 |
| 64 |
(2)小球最多的盒子中小球的个数X的取值为1,2,3.则
P(X=1)=
| ||
| 43 |
| 3 |
| 8 |
| ||||||
| 43 |
| 9 |
| 16 |
| ||
| 43 |
| 1 |
| 16 |
故X的分布列为

所以X的数学期望为E(X)=1×
| 3 |
| 8 |
| 9 |
| 16 |
| 1 |
| 16 |
| 27 |
| 16 |

练习册系列答案
相关题目