题目内容

已知m，n为两个不相等的非零实数，则方程mx-y+n=0与nx2+my2=mn所表示的曲线可能是（　　）
分析：方程mx-y+n=0一定表示直线，方程nx2+my2=mn，如果m，n同正，则表示椭圆，如果一正一负，则表示双曲线，从而可得结论．
解答：解：方程mx-y+n=0表示直线，与坐标轴的交点分别为（0，n），（-
n
m
，0）
若方程nx2+my2=mn表示椭圆，则m，n同为正，∴-
n
m
＜0，故A，B不满足题意；
若方程nx2+my2=mn表示双曲线，则m，n异号，∴-
n
m
＞0，故C符合题意，D不满足题意
故选C
点评：本题考查曲线与方程，考查数形结合的数学思想，判断曲线的类型是关键，属于基础题．
练习册系列答案
相关题目
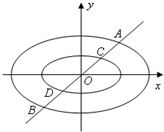精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
精英家教网定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆C1：
x2
4
+y2=1．
（1）若椭圆C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
（2）写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程；若在椭圆Cb上存在两点M、N关于直线y=x+1对称，求实数b的取值范围？
（3）如图：直线y=x与两个“相似椭圆”M：
x2
a2
+
y2
b2
=1和Mλ：
x2
a2
+
y2
b2
=λ2(a＞b＞0，0＜λ＜1)分别交于点A，B和点C，D，试在椭圆M和椭圆Mλ上分别作出点E和点F（非椭圆顶点），使△CDF和△ABE组成以λ为相似比的两个相似三角形，写出具体作法．（不必证明）
（2011•徐汇区三模）定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆C1：
x2
4
+y2=1．
（1）若椭圆C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
（2）写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程；若在椭圆Cb上存在两点M、N关于直线y=x+1对称，求实数b的取值范围？
（3）如图：直线l与两个“相似椭圆”
x2
a2
+
y2
b2
=1和
x2
a2
+
y2
b2
=λ2(a＞b＞0，0＜λ＜1)分别交于点A，B和点C，D，证明：|AC|=|BD|

已知M、N、P是三个相异的平面，a、b是两条相异的直线，则下列命题中不正确的是

[　　]

A．M∩N=a，P⊥M，

B．M∥N，a与M所成的角为α，a与N所成的角为

C．M⊥N，a与M所成的角为α，a与N所成的角为

D．M∥N，

已知M、N、P是三个相异的平面，a、b是两条相异的直线，则下列命题中不正确的是

[　　]

A．M∩N=a，P⊥M，

B．M∥N，a与M所成的角为α，a与N所成的角为

C．M⊥N，a与M所成的角为α，a与N所成的角为

D．M∥N，

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网