题目内容
已知-1＜a＜0，那么-a，-a3，a2的大小关系是（ ）
分析：利用“作差法”和不等式的性质即可得出．
解答：解：∵-1＜a＜0，∴1+a＞0，0＜-a＜1．
∴-a-a2=-a（1+a）＞0，a2-（-a3）=a2（1+a）＞0．
∴-a＞a2＞-a3．
故选B．
∴-a-a2=-a（1+a）＞0，a2-（-a3）=a2（1+a）＞0．
∴-a＞a2＞-a3．
故选B．
点评：本题考查了利用“作差法”比较两个数的大小和不等式的性质，属于基础题．
练习册系列答案
相关题目
已知函数f（x）是定义在R上的偶函数，且f（1-x）=f（-x-3），当0≤x≤2时，f(x)=
，那使f(x)=
成立的x的集合为（ ）
| x |
| 2 |
| 1 |
| 2 |
| A、{x|x=2n，n∈Z} |
| B、{x|x=2n-1，n∈Z} |
| C、{x|x=4n-1，n∈Z} |
| D、{x|x=4n+1，n∈Z} |
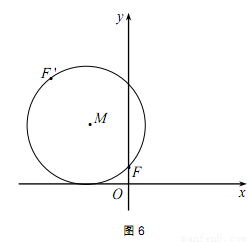
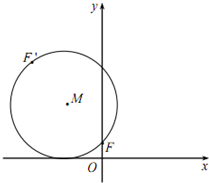（2012•深圳二模）如图，已知动圆M过定点F（0，1）且与x轴相切，点F关于圆心M的对称点为F′，动点F′的轨迹为C．
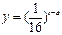（a为常数），如图所示，根据图中提供的信息，回答下列问题：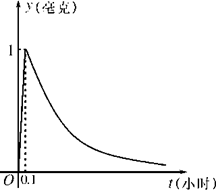 
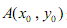是曲线C上的一个定点，过点A任意作两条倾斜角互补的直线，分别与曲线C相交于另外两点P
、Q． 