题目内容
已知过点(0,1)的直线l:xtanα-y-3tanβ=0的斜率为2,则tan(α+β)=
- A.

- B.

- C.

- D.1
D
分析:由题意可得tanα=2,且 0-1-3tanβ=0,求得tanα=2,且 tanβ=- ,利用两角和的正切公式计算 tan(α+β)=
,利用两角和的正切公式计算 tan(α+β)= 的值.
的值.
解答:∵已知过点(0,1)的直线l:xtanα-y-3tanβ=0的斜率为2,
∴tanα=2,且 0-1-3tanβ=0.
解得 tanα=2,且 tanβ=- ,
,
∴tan(α+β)= =
=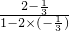 =1,
=1,
故选 D.
点评:本题主要考查两角和的正切公式的应用,属于基础题.
分析:由题意可得tanα=2,且 0-1-3tanβ=0,求得tanα=2,且 tanβ=-
 ,利用两角和的正切公式计算 tan(α+β)=
,利用两角和的正切公式计算 tan(α+β)= 的值.
的值.解答:∵已知过点(0,1)的直线l:xtanα-y-3tanβ=0的斜率为2,
∴tanα=2,且 0-1-3tanβ=0.
解得 tanα=2,且 tanβ=-
 ,
,∴tan(α+β)=
 =
=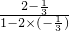 =1,
=1,故选 D.
点评:本题主要考查两角和的正切公式的应用,属于基础题.

练习册系列答案
相关题目



 交于两个不同点M和N.求曲线C在点M、N处切线的交点轨迹.
交于两个不同点M和N.求曲线C在点M、N处切线的交点轨迹.