题目内容
极坐标系与直角坐标系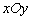 有相同的长度单位,以原点
有相同的长度单位,以原点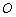 为极点,以
为极点,以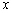 正半轴为极轴,已知曲线
正半轴为极轴,已知曲线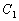 的极坐标方程为
的极坐标方程为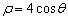 ,曲线
,曲线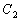 的参数方程是
的参数方程是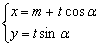 (
(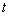 为参数,
为参数,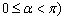 ,射线
,射线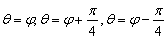 与曲线
与曲线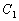 交于极点
交于极点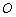 外的三点
外的三点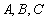
(Ⅰ)求证: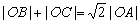 ;
;
(Ⅱ)当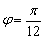 时,
时,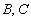 两点在曲线
两点在曲线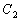 上,求
上,求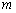 与
与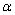 的值.
的值.
(Ⅰ)用坐标法证明 (Ⅱ)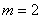

解析试题分析:(1)设点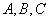 的极坐标分别为
的极坐标分别为
∵点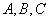 在曲线
在曲线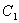 上,∴
上,∴
则 =
=
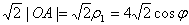 , 所以
, 所以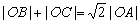
(2)由曲线 的参数方程知曲线
的参数方程知曲线 为倾斜角为
为倾斜角为 且过定点
且过定点 的直线,
的直线,
当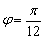 时,B,C点的极坐标分别为
时,B,C点的极坐标分别为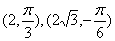
化为直角坐标为 ,
,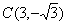 ,
,
∵直线斜率为 ,
, , ∴
, ∴
直线BC的普通方程为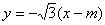 , ∵过点
, ∵过点 ,
,
∴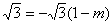 ,解得
,解得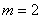
考点:圆的参数方程;直线与圆的位置关系;简单曲线的极坐标方程.
点评:本题考查了极坐标方程、直角坐标方程的转化,参数方程中参数的意义,考查了方程思想.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
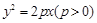 的焦点为
的焦点为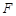 ,点
,点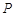 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,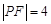 .
.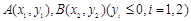 是抛物线上的两点,
是抛物线上的两点,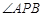 的角平分线与
的角平分线与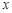 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;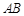 过点
过点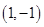 ,求弦
,求弦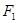 、
、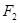 分别为椭圆
分别为椭圆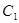 :
: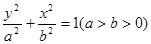 的上、下焦点,其中
的上、下焦点,其中 :
: 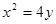 的焦点,点
的焦点,点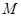 是
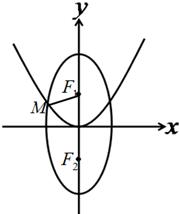
是 。
。
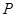 (1,3)和圆
(1,3)和圆 :
: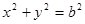 ,过点
,过点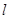 与圆
与圆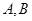 ,在线段
,在线段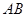 取一点
取一点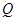 ,满足:
,满足: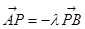 ,
,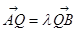 (
(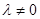 且
且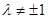 )。
)。 的右焦点为
的右焦点为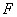 ,右准线为
,右准线为 ,离心率为
,离心率为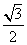 ,点
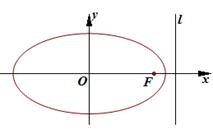
,点 在椭圆上,以
在椭圆上,以 为半径的圆与
为半径的圆与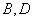 .
.
 是边长为
是边长为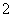 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;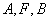 三点在同一条直线
三点在同一条直线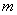 上,且原点到直线
上,且原点到直线 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为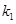 、
、 且
且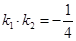
 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线 的距离。(O为坐标原点)
的距离。(O为坐标原点) (
( ,
,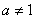 )的图象恒过定点
)的图象恒过定点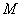 ,椭圆
,椭圆 :
: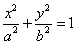 (
(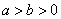 )的左,右焦点分别为
)的左,右焦点分别为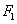 ,
,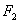 ,直线
,直线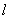 经过点
经过点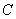 :
: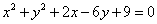 相切.
相切.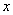 轴上方的交点为
轴上方的交点为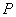 ,且
,且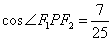 ,求
,求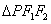 内切圆的方程.
内切圆的方程. 的离心率为
的离心率为 ,右准线方程为
,右准线方程为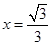 。
。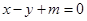 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆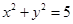 上,求实数m的值。
上,求实数m的值。 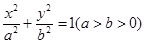 的左右焦点分别为
的左右焦点分别为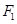 、
、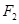 ,由4个点
,由4个点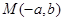 、
、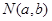 、
、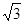 ,面积为
,面积为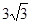 的等腰梯形.
的等腰梯形.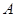 、
、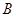 两点,求
两点,求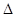
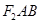 面积的最大值.
面积的最大值.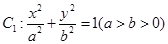 的离心率为
的离心率为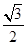 ,
,
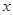 轴被抛物线
轴被抛物线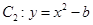 截得的线段长等于
截得的线段长等于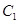 的长半轴长.
的长半轴长.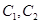 的方程;
的方程;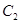 与
与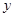 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 的直线
的直线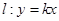
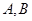 两点,直线
两点,直线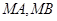 分别与
分别与 .
. 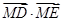 为定值;
为定值;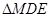 的面积为
的面积为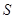 ,试把
,试把 的函数,并求
的函数,并求