题目内容
已知椭圆C短轴的一个端点为(0,1),离心率为 .
.(1)求椭圆的标准方程;
(2)设直线y=x+2交椭圆C于A、B两点,求线段AB的长.
【答案】分析:(1)由椭圆C短轴的一个端点为(0,1),知椭圆的焦点在x轴上,b=1,由 ,知a=3,由此能求出椭圆方程.
,知a=3,由此能求出椭圆方程.
(2)联立方程组 ,得10x2+36x+27=0,由此利用弦长公式能够求出张段AB的长.
,得10x2+36x+27=0,由此利用弦长公式能够求出张段AB的长.
解答:(本小题满分10分)
解:(1)∵椭圆C短轴的一个端点为(0,1),
∴椭圆的焦点在x轴上,b=1,…(2分)
∵ ,
, ,∴得a=3,…(3分)
,∴得a=3,…(3分)
所以其标准方程是: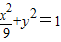 .…(4分)
.…(4分)
(2)联立方程组 ,消去y得,10x2+36x+27=0.…(5分)
,消去y得,10x2+36x+27=0.…(5分)
△=362-4×10×27>0
设A(x1,y1),B(x2,y2), ,
,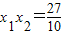 ,…(7分)
,…(7分)
所以|AB|=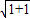 •
• =
=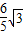 .…(10分)
.…(10分)
点评:本题考查椭圆方程的求法,考查弦长公式的应用,解题时要认真审题,仔细解答.
 ,知a=3,由此能求出椭圆方程.
,知a=3,由此能求出椭圆方程.(2)联立方程组
 ,得10x2+36x+27=0,由此利用弦长公式能够求出张段AB的长.
,得10x2+36x+27=0,由此利用弦长公式能够求出张段AB的长.解答:(本小题满分10分)
解:(1)∵椭圆C短轴的一个端点为(0,1),
∴椭圆的焦点在x轴上,b=1,…(2分)
∵
 ,
, ,∴得a=3,…(3分)
,∴得a=3,…(3分)所以其标准方程是:
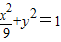 .…(4分)
.…(4分)(2)联立方程组
 ,消去y得,10x2+36x+27=0.…(5分)
,消去y得,10x2+36x+27=0.…(5分)△=362-4×10×27>0
设A(x1,y1),B(x2,y2),
 ,
,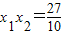 ,…(7分)
,…(7分)所以|AB|=
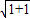 •
• =
=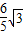 .…(10分)
.…(10分)点评:本题考查椭圆方程的求法,考查弦长公式的应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
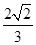 ,
, 交椭圆C于A、B两点,求线段AB的长.
交椭圆C于A、B两点,求线段AB的长.