题目内容
设函数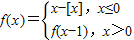 ,其中[x]表示不超过x的最大整数,如[-1.2]=-2,[1.2]=1,[1]=1,若f(x)=kx+k(k>0)有三个不同的根,则实数k的取值范围是( )
,其中[x]表示不超过x的最大整数,如[-1.2]=-2,[1.2]=1,[1]=1,若f(x)=kx+k(k>0)有三个不同的根,则实数k的取值范围是( )A.
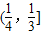
B.
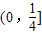
C.
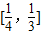
D.
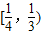
【答案】分析:若f(x)=kx+k有三个不同的根,则函数y=f(x)的图象与y=kx+k的图象有三个交点,我们画出函数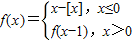 的图象,结合y=kx+k的图象恒过(-1,0)点,数形结合,易分析出k的取值范围.
的图象,结合y=kx+k的图象恒过(-1,0)点,数形结合,易分析出k的取值范围.
解答:解:∵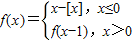
∴函数的图象如下图所示:

∵y=kx+k=k(x+1),故函数图象一定过(-1,0)点
若f(x)=kx+k有三个不同的根,
则y=kx+k与y=f(x)的图象有三个交点
当y=kx+k过(2,1)点是k= ,
,
当y=kx+k过(3,1)点是k= ,
,
故f(x)=kx+k有三个不同的根,则实数k的取值范围是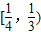
故选D
点评:本题考查的知识点是根据根的存在性及根的个数的判断,其中将方程的根转化为函数的零点,然后利用图象法结合数形结合的思想,分析函数图象交点与k的关系是解答本题的关键.
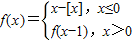 的图象,结合y=kx+k的图象恒过(-1,0)点,数形结合,易分析出k的取值范围.
的图象,结合y=kx+k的图象恒过(-1,0)点,数形结合,易分析出k的取值范围.解答:解:∵
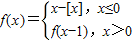
∴函数的图象如下图所示:

∵y=kx+k=k(x+1),故函数图象一定过(-1,0)点
若f(x)=kx+k有三个不同的根,
则y=kx+k与y=f(x)的图象有三个交点
当y=kx+k过(2,1)点是k=
 ,
,当y=kx+k过(3,1)点是k=
 ,
,故f(x)=kx+k有三个不同的根,则实数k的取值范围是
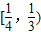
故选D
点评:本题考查的知识点是根据根的存在性及根的个数的判断,其中将方程的根转化为函数的零点,然后利用图象法结合数形结合的思想,分析函数图象交点与k的关系是解答本题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表:
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表: (2013•枣庄一模)设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
(2013•枣庄一模)设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系: 将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表:
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表: (其中x>0),设该数表的第n行的所有数之和为bn,
(其中x>0),设该数表的第n行的所有数之和为bn, .
. (其中x>0),设该数表的第n行的所有数之和为bn,
(其中x>0),设该数表的第n行的所有数之和为bn, .
.