题目内容
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表:记aij是这个数表的第i行第j列的数.例如a43=17
(Ⅰ) 求该数表前5行所有数之和S;
(Ⅱ)2009这个数位于第几行第几列?
(Ⅲ)已知函数
 (其中x>0),设该数表的第n行的所有数之和为bn,
(其中x>0),设该数表的第n行的所有数之和为bn,数列{f(bn)}的前n项和为Tn,求证
 .
.
【答案】分析:(Ⅰ)由题设条件,得用等到差数列求和公式直接计算即可.
(Ⅱ)由2009=2×1005-1,知2009是正奇数列的第1005个数.设2009这个数位于第m行,前m-1行共有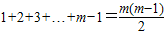 个数,所以
个数,所以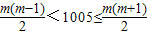 ,由此能求出2009这个数位于第几行第几列.
,由此能求出2009这个数位于第几行第几列.
(Ⅲ)第n行的第一个数为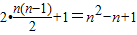 ,第n行各数形成以n2-n+1为首项,2为公差的等差数列
,第n行各数形成以n2-n+1为首项,2为公差的等差数列
故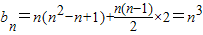 .所以
.所以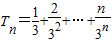 ,再由错位相减法能够证明
,再由错位相减法能够证明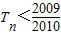 .
.
解答:解:(Ⅰ)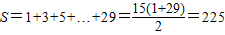 …(3分)
…(3分)
(Ⅱ)∵2009=2×1005-1,
∴2009是正奇数列的第1005个数.…(5分)
设2009这个数位于第m行,前m-1行共有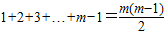 个数,…(7分)
个数,…(7分)
则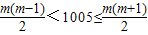 ,
,
又m∈N+,∴m=45…(8分)
故前44行共有990个数,
第45行的第1个数是2×991-1=1981…(9分)
2009=1981+2(n-1),∴n=15
故2009位于第45行第15列.…(10分)
(Ⅲ)证明:第n行的第一个数为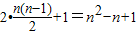 ,
,
第n行各数形成以n2-n+1为首项,2为公差的等差数列
故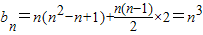 …(12分)
…(12分)
∴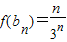
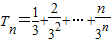 …(1)
…(1)
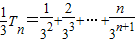 …(2)
…(2)
(1)-(2)整理得: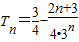 <
<
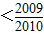 .…(14分)
.…(14分)
点评:本题考查数列与不等式的综合运用,综合性强,难度较大,容易出错.解题时要认真审题,仔细解答,注意错位相减法的合理运用.
(Ⅱ)由2009=2×1005-1,知2009是正奇数列的第1005个数.设2009这个数位于第m行,前m-1行共有
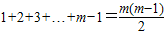 个数,所以
个数,所以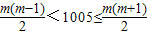 ,由此能求出2009这个数位于第几行第几列.
,由此能求出2009这个数位于第几行第几列.(Ⅲ)第n行的第一个数为
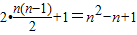 ,第n行各数形成以n2-n+1为首项,2为公差的等差数列
,第n行各数形成以n2-n+1为首项,2为公差的等差数列故
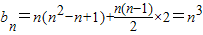 .所以
.所以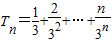 ,再由错位相减法能够证明
,再由错位相减法能够证明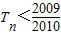 .
.解答:解:(Ⅰ)
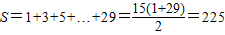 …(3分)
…(3分)(Ⅱ)∵2009=2×1005-1,
∴2009是正奇数列的第1005个数.…(5分)
设2009这个数位于第m行,前m-1行共有
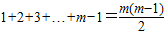 个数,…(7分)
个数,…(7分)则
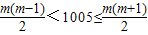 ,
,又m∈N+,∴m=45…(8分)
故前44行共有990个数,
第45行的第1个数是2×991-1=1981…(9分)
2009=1981+2(n-1),∴n=15
故2009位于第45行第15列.…(10分)
(Ⅲ)证明:第n行的第一个数为
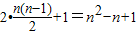 ,
,第n行各数形成以n2-n+1为首项,2为公差的等差数列
故
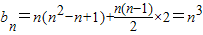 …(12分)
…(12分)∴
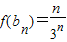
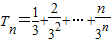 …(1)
…(1)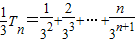 …(2)
…(2)(1)-(2)整理得:
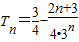 <
<
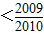 .…(14分)
.…(14分)点评:本题考查数列与不等式的综合运用,综合性强,难度较大,容易出错.解题时要认真审题,仔细解答,注意错位相减法的合理运用.

练习册系列答案
相关题目
 将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表:
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表: 将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表:
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表: (其中x>0),设该数表的第n行的所有数之和为bn,
(其中x>0),设该数表的第n行的所有数之和为bn, .
.