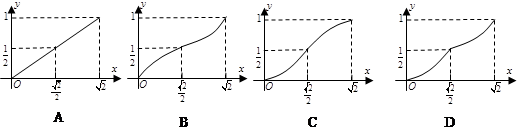题目内容
下列函数中,既是偶函数,又在区间 上是减函数的是( )
上是减函数的是( )
A. | B. | C. | D. |
B
解析试题分析:显然 既是偶函数,又在区间
既是偶函数,又在区间 上是减函数,故选B.
上是减函数,故选B. 在区间
在区间 上是增函数;
上是增函数;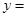
 和
和 都不是偶函数.
都不是偶函数.
考点:函数的单调性与奇偶性.

练习册系列答案
相关题目
不等式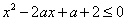 的解集为
的解集为 ,如果
,如果 ,求实数
,求实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数f(x)的定义域为[-1,5],部分对应值如下表:
| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
f(x)的导函数y=f′(x)的图象如图所示.

下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中真命题的个数是( )
A.4 B.3 C.2 D.1
函数y=2ax﹣1(0<a<1)的图象一定过点( )
| A.(1,1) | B.(1,2) |
| C.(2,0) | D.(2,﹣1) |
已知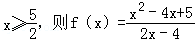 有( )
有( )
A.最大值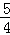 | B.最小值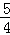 | C.最大值1 | D.最小值1 |
函数y=x2+b x+c(x∈[0,+∞))是单调函数的充要条件是( )
| A.b≥0 | B.b≤0 | C.b>0 | D.b<0 |
函数 图象上关于原点对称点共有( )
图象上关于原点对称点共有( )
| A.0对 | B.1对 | C.2对 | D.3对 |
若函数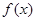 满足
满足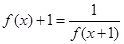 ,当x∈[0,1]时,
,当x∈[0,1]时,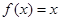 ,若在区间(-1,1]上, 方程
,若在区间(-1,1]上, 方程 有两个实数解,则实数m的取值范围是
有两个实数解,则实数m的取值范围是
A.0<m≤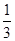 | B.0<m<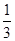 |
C.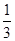 <m≤l <m≤l | D.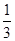 <m<1 <m<1 |
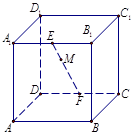
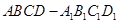 的棱长为
的棱长为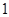 ,
, 分别是棱
分别是棱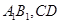 的中点,点
的中点,点 是
是 的动点,
的动点,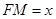 ,过点
,过点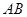 的平面将正方体分成上下两部分,记下面那部分的体积为
的平面将正方体分成上下两部分,记下面那部分的体积为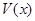 ,则函数
,则函数