Question

已知球面上有三点A、B．C，此三点构成一个边长为1的等边三角形，球心到平面ABC的距离等于球半径的

1

3

，则球半径是（　　）

• A．

  3

• B．

  1

  3

• C．

  6

  4

• D．

  3

  2

Answer 1

分析：根据△ABC是一个边长为l的等边三角形，得到它的外心到顶点的距离，即经过A、B、C的球小圆半径．再根据球心到平面ABC的距离等于球半径的 

1

3

，结合球的截面圆性质和勾股定理建立关系式，解之即得球半径的值．

解答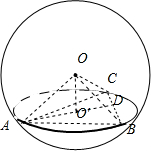：解：∵△ABC是一个边长为l的等边三角形，∴△ABC的高AD=

3

2

．
设△ABC的外接圆圆心设为O'，得到AO'=

2

3

AD=

3

3

再设球心为O，因为球心O到平面ABC的距离等于球半径的

1

3

，
所以OO'=

1

3

OA，
Rt△OO'A中，O'A²+OO'²=OA²，即（

3

3

）2+

1

9

OA²=OA²
∴

8

9

OA²=

1

3

，故OA=

6

4

，即球半径是

6

4

．
故选：C．

点评：本题给出球截面圆的内接等边三角形边长和球心到截面的距离，求它的半径，着重考查了球的截面圆的性质和空间距离计算的知识点，属于基础题．