题目内容
已知球面上有三点A，B，C且AB=6cm，BC=8cm，CA=10cm，若球心到平面ABC距离为7cm，则此球的表面积为
296π
296π
cm3．分析：欲求球的表面积，即求求的半径，先作出球心到平面ABC的距离，注意到三角形ABC是直角三角形，所求距离即为OA的长，最后根据球的面积公式解之即可．
解答：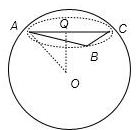
解：由题意得，球心O在平面ABC上的射影是直角三角形ABC斜边AC的中点，
OA的长即为所求．
在直角三角形AOQ中，
r=OA=
=
．
此球的表面积为4πr2=4π×74=296π
故答案为：296π．
解：由题意得，球心O在平面ABC上的射影是直角三角形ABC斜边AC的中点，OA的长即为所求．
在直角三角形AOQ中，
r=OA=
| 72+52 |
| 74 |
此球的表面积为4πr2=4π×74=296π
故答案为：296π．
点评：本题主要考查了点、线、面间的距离计算，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目