题目内容
三角形三边长分别为k2+k+1,k2-1,2k+1,求这个三角形的最大角.
思路分析:要求最大角,首先要判断哪一条是最长的边,大边对大角;然后利用余弦定理,求最大角的余弦值.
解:由题意知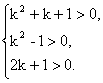
解之得k>1.
∵k2+k+1-(k2-1)>0,
k2+k+1-(2k+1)=k2-k=k(k-1)>0,
∴最大边是k2+k+1.设对角为A,
由余弦定理得
cosA=![]()
=-![]() .∴A=120°.
.∴A=120°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
三角形三边长分别为k2+k+1,k2-1,2k+1,求这个三角形的最大角.
思路分析:要求最大角,首先要判断哪一条是最长的边,大边对大角;然后利用余弦定理,求最大角的余弦值.
解:由题意知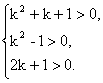
解之得k>1.
∵k2+k+1-(k2-1)>0,
k2+k+1-(2k+1)=k2-k=k(k-1)>0,
∴最大边是k2+k+1.设对角为A,
由余弦定理得
cosA=![]()
=-![]() .∴A=120°.
.∴A=120°.

 名校课堂系列答案
名校课堂系列答案