题目内容
将边长为1的正方体木块ABCD-A1B1C1D1沿平面BB1D1D锯开后得到两个三棱柱,将这两个三棱柱重新进行拼接,组成一个新的三棱柱,则新的三棱柱的表面积是
5+2
;4+2
;6+2
| 2 |
| 2 |
| 2 |
5+2
;4+2
;6+2
.(写出所有可能的情况)| 2 |
| 2 |
| 2 |
分析:求得由这两个三棱柱组成的简单几何体可以是 ①高为2的直三棱柱;②高为1的直三棱柱;③直四棱柱,且四棱柱的前后面是矩形(长
,宽为1)、左右面是边长为1的正方形,上下面是平行四边形,再分别计算表面积即可.
| 2 |
解答:解:如图,由这两个三棱柱组成的简单几何体可以是 ①高为2的直三棱柱;②高为1的直三棱柱;③直四棱柱,且四棱柱的前后面是矩形(长
,宽为1)、左右面是边长为1的正方形,上下面是平行四边形.
①高为2的直三棱柱的表面面积为 2(
×1×1)+2(2×1)+2×
=5+2
.
②高为1的直三棱柱的表面面积为 2(
×
×
)+2(1×
)+1×2=4+2
.
③直四棱柱的表面面积为 2(
×1)+2(1×1)+2(1×2 )=6+2
.
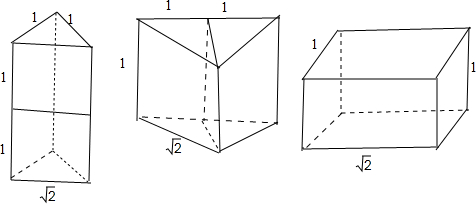
故答案为:5+2
;4+2
;6+2
| 2 |
①高为2的直三棱柱的表面面积为 2(
| 1 |
| 2 |
| 2 |
| 2 |
②高为1的直三棱柱的表面面积为 2(
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
③直四棱柱的表面面积为 2(
| 2 |
| 2 |

故答案为:5+2
| 2 |
| 2 |
| 2 |
点评:本题考查棱柱的表面积,考查学生空间想象能力,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 沿平面
沿平面 锯开后得到两个三棱柱,那么由这两个三棱柱组成的简单几何体有______________种,它们的表面积分别是_______________.(写出所有可能的情况,原正方体除外)
锯开后得到两个三棱柱,那么由这两个三棱柱组成的简单几何体有______________种,它们的表面积分别是_______________.(写出所有可能的情况,原正方体除外)