题目内容
有以下命题:设an1,an2,…anm是公差为d的等差数列{an}中任意m项,若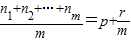 (p∈N*,r∈N且r<m),则
(p∈N*,r∈N且r<m),则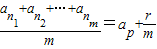 d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.
d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.(1)已知等差数列{an}的通项公式为an=2n,根据上述命题,则a1,a3,a10,a18的等差平均项为: ;
(2)将上述真命题推广到各项为正实数的等比数列中:设an1,an2,…anm是公比为q的等比数列{an}中任意m项,若
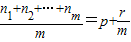 (p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.
(p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.
【答案】分析:(1)利用新定义,结合等差数列{an}的通项公式为an=2n,可求a1,a3,a10,a18的等差平均项;
(2)等差数列研究和问题,类比等比数列则研究积问题,通过计算可以得结论.
解答:解:(1)由题意,a1,a3,a10,a18的等差平均项为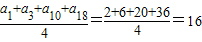 ;
;
(2)由题意,类比得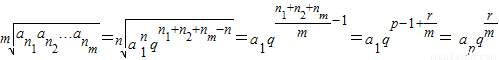
故答案为16;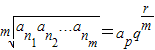
点评:本题考查新定义的理解,同时考查了类比思想的运用,关键是理解新定义,同时明确等差数列与等比数列之间类比得方法.
(2)等差数列研究和问题,类比等比数列则研究积问题,通过计算可以得结论.
解答:解:(1)由题意,a1,a3,a10,a18的等差平均项为
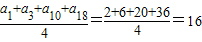 ;
;(2)由题意,类比得
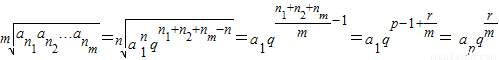
故答案为16;
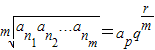
点评:本题考查新定义的理解,同时考查了类比思想的运用,关键是理解新定义,同时明确等差数列与等比数列之间类比得方法.

练习册系列答案
相关题目
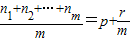 (p∈N*,r∈N且r<m),则
(p∈N*,r∈N且r<m),则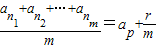 d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.
d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.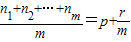 (p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.
(p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项. (p∈N*,r∈N且r<m),则
(p∈N*,r∈N且r<m),则 d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.
d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项. (p∈N*,r∈N且r<m),则( );特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.
(p∈N*,r∈N且r<m),则( );特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.