题目内容
(文)(1)设复数z满足z•
=9,且(1+2i)z为纯虚数,求复数z;
(2)设复数z1,z2满足|z1|=|z2|=1,且|z1+z2|=
,求|z1-z2|.
. |
| z |
(2)设复数z1,z2满足|z1|=|z2|=1,且|z1+z2|=
| 2 |
分析:(1)利用复数的运算法则和纯虚数的定义即可得出;
(2)利用复数模的计算公式和复数的运算性质即可得出.
(2)利用复数模的计算公式和复数的运算性质即可得出.
解答:解:(1)设z=a+bi(a,b∈R),则z•
=a2+b2=9.
∵(1+2i)z=a-2b+(2a+b)i为纯虚数,∴a-2b=0,2a+b≠0.
联立
.
解得
或
.
∴z=
+
i或z=-
-
i.
(2)∵|z1+z2|=
,
∴|z1+z2|2=(z1+z2)•
=2,
∴2+z1
+
z2=2.得z1
+
z2=0.
∴|z1-z2|2=2-(z1
+
z2)=2.
又|z1-z2|>0,故|z1-z2|=
.
. |
| z |
∵(1+2i)z=a-2b+(2a+b)i为纯虚数,∴a-2b=0,2a+b≠0.
联立
|
解得
|
|
∴z=
6
| ||
| 5 |
3
| ||
| 5 |
6
| ||
| 5 |
3
| ||
| 5 |
(2)∵|z1+z2|=
| 2 |
∴|z1+z2|2=(z1+z2)•
. |
| (z1+z2) |
∴2+z1
. |
| z2 |
. |
| z1 |
. |
| z2 |
. |
| z1 |
∴|z1-z2|2=2-(z1
. |
| z2 |
. |
| z1 |
又|z1-z2|>0,故|z1-z2|=
| 2 |
点评:熟练掌握复数的运算法则和纯虚数的定义、复数模的计算公式设解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
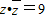 ,且(1+2i)z为纯虚数,求复数z;
,且(1+2i)z为纯虚数,求复数z;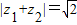 ,求|z1-z2|.
,求|z1-z2|.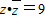 ,且(1+2i)z为纯虚数,求复数z;
,且(1+2i)z为纯虚数,求复数z;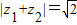 ,求|z1-z2|.
,求|z1-z2|.