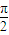题目内容
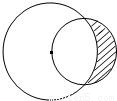
如图所示,一个半径为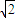 的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )
的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )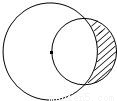
A.1
B.2
C.
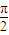
D.4-π
【答案】分析:先由余弦定理求得∠O2O1A,进而求得∠AO2B,通过角的关系,得出A、B、O2在一直线上,将阴影部分转化为扇形解决.
解答: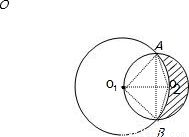 解:连接AB、O1A、O2A、O1B、O2B、O1O2,
解:连接AB、O1A、O2A、O1B、O2B、O1O2,
cos∠O2O1A= (O1O22+O1A2-O2A2)×O1O2×O1A
(O1O22+O1A2-O2A2)×O1O2×O1A
=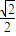
∴∠O2O1A=45°
∴∠AO1B=45°×2=90°,∠AO2B=2∠AO1B=180°
又O2A=O1O2,∠O2AO1=45°
∴∠AO2O1=90°,O1O2⊥AB
∴A、B、O2在一直线上
∴AB=2O1O2=2×2,O1O2=2
又O1A=2
图中阴影部分的面积为:
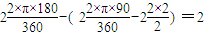
故选B.
点评:本题主要考查圆与圆的位置关系和图形的转化能力.
解答:
 解:连接AB、O1A、O2A、O1B、O2B、O1O2,
解:连接AB、O1A、O2A、O1B、O2B、O1O2,cos∠O2O1A=
 (O1O22+O1A2-O2A2)×O1O2×O1A
(O1O22+O1A2-O2A2)×O1O2×O1A=
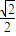
∴∠O2O1A=45°
∴∠AO1B=45°×2=90°,∠AO2B=2∠AO1B=180°
又O2A=O1O2,∠O2AO1=45°
∴∠AO2O1=90°,O1O2⊥AB
∴A、B、O2在一直线上
∴AB=2O1O2=2×2,O1O2=2
又O1A=2
图中阴影部分的面积为:
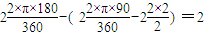
故选B.
点评:本题主要考查圆与圆的位置关系和图形的转化能力.

练习册系列答案
相关题目
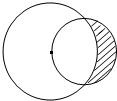 如图所示,一个半径为
如图所示,一个半径为| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4-π |
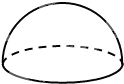 如图所示是一个半径等于2的半球,现过半球底面的中心作一个与底面成90°的截面,则此截面的面积为( )
如图所示是一个半径等于2的半球,现过半球底面的中心作一个与底面成90°的截面,则此截面的面积为( )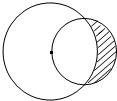 如图所示,一个半径为
如图所示,一个半径为 的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为
的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为
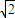 的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )
的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )