题目内容
下列五个命题中,正确的有几个?( )①函数y=
 与y=(
与y=(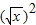 是同一函数;
是同一函数;②若集合A={x|kx2+4x+4=0}中只有一个元素,则k=1;
③集合M={(x,y)|2x-y=3},N={(x,y)|x+y=0},那么集合M∩N={1,-1};
④方程x2+4x+4=0的解集中含有一个元素;
⑤Φ?A.
A.1
B.2
C.3
D.4
【答案】分析:①由同一函数的概念,同一函数要求对应法则、值域和对应关系均相同,而y=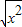 的定义域为R,y=
的定义域为R,y= 的定义域为x≥0,故错误.
的定义域为x≥0,故错误.
②中应考虑到k=0和k≠0两种情况;
③由已知中集合M={(x,y)|2x-y=3},N={(x,y)|x+y=0},表示两条相交直线上的点组成的点集,故集合M∩N即为只含两条直线交点一个元素的点集,联立方程求出交点坐标,即可得到答案.
④解出方程x2+4x+4=0的解集即可得出答案.
⑤根据空集的含义进行判断即得.
解答:解:①中y=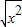 的定义域为R,y=
的定义域为R,y= 的定义域为x≥0,故错误
的定义域为x≥0,故错误
②中k=0时A={-1}符合要求,故②错误
③∵集合M={(x,y)|2x-y=3},N={(x,y)|x+y=0},
∴M∩N={(x,y)| }={(1,-1)},而不是M∩N={1,-1};错误
}={(1,-1)},而不是M∩N={1,-1};错误
④方程x2+4x+4=0的解集为{-2},其中含有一个元素-2,正确.
⑤空集是任何非空集合的真子集,但A不一定是非空集合,故错.
∴五个命题中,正确的有1个.
故选A.
点评:本题考查命题真假的判断、函数的概念、空集的概念、集合的表示等知识,属基本题型的考查.
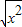 的定义域为R,y=
的定义域为R,y= 的定义域为x≥0,故错误.
的定义域为x≥0,故错误.②中应考虑到k=0和k≠0两种情况;
③由已知中集合M={(x,y)|2x-y=3},N={(x,y)|x+y=0},表示两条相交直线上的点组成的点集,故集合M∩N即为只含两条直线交点一个元素的点集,联立方程求出交点坐标,即可得到答案.
④解出方程x2+4x+4=0的解集即可得出答案.
⑤根据空集的含义进行判断即得.
解答:解:①中y=
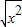 的定义域为R,y=
的定义域为R,y= 的定义域为x≥0,故错误
的定义域为x≥0,故错误②中k=0时A={-1}符合要求,故②错误
③∵集合M={(x,y)|2x-y=3},N={(x,y)|x+y=0},
∴M∩N={(x,y)|
 }={(1,-1)},而不是M∩N={1,-1};错误
}={(1,-1)},而不是M∩N={1,-1};错误④方程x2+4x+4=0的解集为{-2},其中含有一个元素-2,正确.
⑤空集是任何非空集合的真子集,但A不一定是非空集合,故错.
∴五个命题中,正确的有1个.
故选A.
点评:本题考查命题真假的判断、函数的概念、空集的概念、集合的表示等知识,属基本题型的考查.

练习册系列答案
相关题目