题目内容
下列五个命题中,正确的命题的序号是
①函数y=tan
的图象的对称中心是(kπ,0),k∈Z;
②f(x)在(a,b)上连续,x0∈(a,b)且f(x0)=0 则f(a)f(b)<0;
③函数y=3sin(2x+
)的图象可由函数y=3sin2x的图象向右平移
个单位得到;
④f(x)在R上的导数f′(x),且xf′(x)-f(x)<0,则
<f(1);
⑤函数y=ln(1+2cos2x)的递减区间是[kπ,kπ+
](k∈Z).
①④
①④
.①函数y=tan
| x |
| 2 |
②f(x)在(a,b)上连续,x0∈(a,b)且f(x0)=0 则f(a)f(b)<0;
③函数y=3sin(2x+
| π |
| 3 |
| π |
| 3 |
④f(x)在R上的导数f′(x),且xf′(x)-f(x)<0,则
| f(2) |
| 2 |
⑤函数y=ln(1+2cos2x)的递减区间是[kπ,kπ+
| π |
| 4 |
分析:根据正切函数的对称性,可判断①;根据零点存在定理的逆命题不一定成立,可判断②;根据函数图象的平移变换法则,可判断③;构造函数g(x)=
,利用导数法判断其单调性,可判断④;根据复合函数单调性及对数函数和余弦函数的图象和性质,可得答案.
| f(x) |
| x |
解答:解:令
=
,k∈Z,得x=kπ,k∈Z,故函数y=tan
的图象的对称中心是(kπ,0),k∈Z,即①正确;
由f(x0)=0可得x0为函数f(x)的零点,但若x0为函数f(x)的不变号零点,则f(a)f(b)<0不一定成立,即②错误;
函数y=3sin2x的图象向右平移
个单位得到y=3sin2(x+
)=函数y=3sin(2x
)的图象,故③错误;
令g(x)=
,则g′(x)=
,由f′(x)x-f(x)<0可得:g′(x)<0恒成立,故
<f(1),故④正确;
函数y=ln(1+2cos2x)的递减区间是[kπ,kπ+
),(k∈Z),故⑤错误.
故答案为:①④
| x |
| 2 |
| kπ |
| 2 |
| x |
| 2 |
由f(x0)=0可得x0为函数f(x)的零点,但若x0为函数f(x)的不变号零点,则f(a)f(b)<0不一定成立,即②错误;
函数y=3sin2x的图象向右平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
令g(x)=
| f(x) |
| x |
| f′(x)x-f(x) |
| x2 |
| f(2) |
| 2 |
函数y=ln(1+2cos2x)的递减区间是[kπ,kπ+
| π |
| 3 |
故答案为:①④
点评:本题以命题的真假判断与应用为载体,考查了三角函数的对称性,函数的零点,函数图象的平移变换,函数的单调性等知识点,综合性强,但难度不大.

练习册系列答案
相关题目
 与y=(
与y=(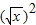 是同一函数;
是同一函数;