题目内容
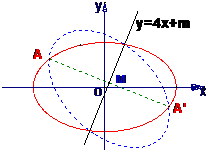
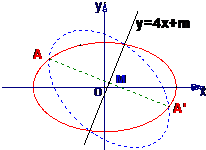 试确定m的取值范围,使得椭圆
试确定m的取值范围,使得椭圆 上有不同两点关于直线y=4x+m对称.
上有不同两点关于直线y=4x+m对称.
解:设交点是A(x1,y1)B(x2,y2)中点坐标是(x中,y中)AB直线方程设为y=- x+b
x+b
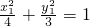 ①
①
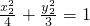 ②
②
y1=- x1+b③
x1+b③
y2=- x2+b④
x2+b④
①-②,得
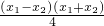 +
+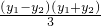 =0
=0
③-④,得
y1-y2=- (x1-x2)把y1-y2整体代入上式,提取公因式(x1-x2)得
(x1-x2)把y1-y2整体代入上式,提取公因式(x1-x2)得
(x1-x2)(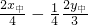 )=0
)=0
由于x1不等于x2,所以,
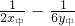 =0
=0
又 y中=4x中+m
解得 x中=-m y中=-3m
∵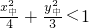
∴m2<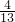
∴- <m<
<m<
分析:设交点是A(x1,y1)B(x2,y2)中点坐标是(x中,y中)AB直线方程设为y=- x+b,把A,B点坐标分别代入椭圆方程和直线方程,分别相减联立后求得
x+b,把A,B点坐标分别代入椭圆方程和直线方程,分别相减联立后求得 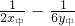 =0,解得 x中和y中,进而根据
=0,解得 x中和y中,进而根据 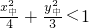 求得m的范围.
求得m的范围.
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的思路是利用两个对称点的中点在椭圆的内部,进而求得m的范围.
 x+b
x+b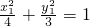 ①
①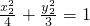 ②
②y1=-
 x1+b③
x1+b③y2=-
 x2+b④
x2+b④①-②,得
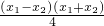 +
+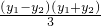 =0
=0③-④,得
y1-y2=-
 (x1-x2)把y1-y2整体代入上式,提取公因式(x1-x2)得
(x1-x2)把y1-y2整体代入上式,提取公因式(x1-x2)得(x1-x2)(
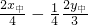 )=0
)=0由于x1不等于x2,所以,
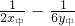 =0
=0又 y中=4x中+m
解得 x中=-m y中=-3m
∵
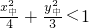
∴m2<
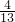
∴-
 <m<
<m<

分析:设交点是A(x1,y1)B(x2,y2)中点坐标是(x中,y中)AB直线方程设为y=-
 x+b,把A,B点坐标分别代入椭圆方程和直线方程,分别相减联立后求得
x+b,把A,B点坐标分别代入椭圆方程和直线方程,分别相减联立后求得 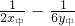 =0,解得 x中和y中,进而根据
=0,解得 x中和y中,进而根据 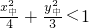 求得m的范围.
求得m的范围.点评:本题主要考查了直线与圆锥曲线的综合问题.解题的思路是利用两个对称点的中点在椭圆的内部,进而求得m的范围.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目