题目内容
若集合
，集合
，则“
”是“
”的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
A
解析试题分析：若，则=
，又集合，所以；
若，则
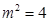，所以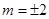
。
考点：集合的运算；充分、必要、充要条件；
点评：本题以充分必要条件的判断为载体，考查了两个集合的简单运算，属于基础题．
练习册系列答案
相关题目
设集合M=
，N=
，则M∩N=（ ）
| A． | B． | C． | D． |
设集合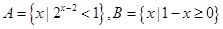
，则A∩B等于（ ）
A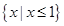． | B． |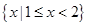
C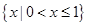． | D． |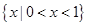
下列各组对象能构成集合的有（ ）
（1）所有的正方体 （2）温州市区内的所有大超市
（3）所有的数学难题 （4）出名的舞蹈家
（5）某工厂2012年生产的所有产品 （6）直角坐标平面坐标轴上所有的点
| A．(1)(3) (5) | B．(1)(2)(4) |
| C．(1)(5)(6) | D．(2)(4)(6) |
已知集合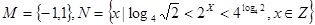 
，则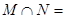
（ ）
A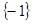． | B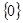． | C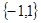． | D． |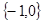
设集合
，
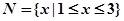，则
（ ）
A． | B． | C． | D． |
已知集合
， 
，则
( )
A． | B． | C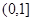． | D． |
巳知全集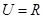
，
是虚数单位，集合
（整数集）和
的关系韦恩（Ｖenn）图如图所示，则阴影部分所示的集合的元素共有（ ）
| A．３个 | B．２个 | C．１个 | D．无穷个 |
已知集合
，
，则
为 （ ）.
A． | B． | C． | D．  |