题目内容
已知复数z=3-2i(1)求
 ;
;(2)若复数az+a2-i在复平面内的对应点在第二象限,求实数a的取值范围.
【答案】分析:(1)依题意,可求得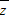 -i,再取模即可;
-i,再取模即可;
(2)由于az+a2-i=a2+3a+(-2a+1)i,根据复数代数表示法的几何意义解关于a的不等式组即可求得实数a的取值范围.
解答:解:(1)∵复数z=3-2i,
∴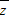 =3+2i,
=3+2i,
∴|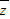 -i|=|3+i|=
-i|=|3+i|=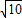 ;
;
(2)∵az+a2-i=a2+3a+(-2a+1)i在复平面内的对应点在第二象限,
∴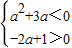 ,
,
解得:-3<a<0.
∴实数a的取值范围是:-3<a<0.
点评:本题考查复数的代数表示法及其几何意义,考查复数求模,考查不等式思想,属于中档题.
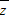 -i,再取模即可;
-i,再取模即可;(2)由于az+a2-i=a2+3a+(-2a+1)i,根据复数代数表示法的几何意义解关于a的不等式组即可求得实数a的取值范围.
解答:解:(1)∵复数z=3-2i,
∴
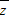 =3+2i,
=3+2i,∴|
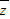 -i|=|3+i|=
-i|=|3+i|=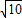 ;
;(2)∵az+a2-i=a2+3a+(-2a+1)i在复平面内的对应点在第二象限,
∴
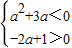 ,
,解得:-3<a<0.
∴实数a的取值范围是:-3<a<0.
点评:本题考查复数的代数表示法及其几何意义,考查复数求模,考查不等式思想,属于中档题.

练习册系列答案
相关题目
已知复数z=-3+2i(i为虚数单位)是关于x的方程2x2+px+q=0(p,q为实数)的一个根,则p+q的值为( )
| A、22 | B、36 | C、38 | D、42 |