题目内容
设函数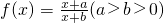
，求f（ x ）的单调区间，并证明f（ x ）在其单调区间上的单调性．
解：函数
的定义域为（-∞，-b）∪（-b，+∞）．
f（x）在（-∞，-b）内是减函数，f（x）在（-b，+∞）内也是减函数．
证明f（x）在（-b，+∞）内是减函数．
取x1，x2∈（-b，+∞），且x1＜x2，那么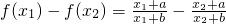
=
，
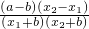∵a-b＞0，x2-x1＞0，（x1+b）（x2+b）＞0，
∴f（x1）-f（x2）＞0，
即f（x）在（-b，+∞）内是减函数．
同理可证f（x）在（-∞，-b）内是减函数．
分析：判断函数的单调性可以通过定义做，也可利用导函数做．
点评：本小题主要考查函数的单调性及不等式的基础知识，考查数学推理判断能力．
的定义域为（-∞，-b）∪（-b，+∞）．f（x）在（-∞，-b）内是减函数，f（x）在（-b，+∞）内也是减函数．
证明f（x）在（-b，+∞）内是减函数．
取x1，x2∈（-b，+∞），且x1＜x2，那么
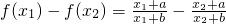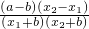=，∵a-b＞0，x2-x1＞0，（x1+b）（x2+b）＞0，
∴f（x1）-f（x2）＞0，
即f（x）在（-b，+∞）内是减函数．
同理可证f（x）在（-∞，-b）内是减函数．
分析：判断函数的单调性可以通过定义做，也可利用导函数做．
点评：本小题主要考查函数的单调性及不等式的基础知识，考查数学推理判断能力．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
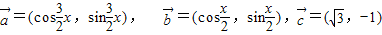，其中x∈R，
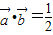时，求x值的集合；
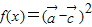，求f（x）的最小正周期及其单调增区间．
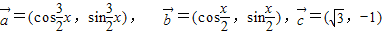，其中x∈R，
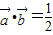时，求x值的集合；
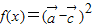，求f（x）的最小正周期及其单调增区间．
，
，
．
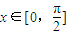，求x的值；
，求f（x）的最大值．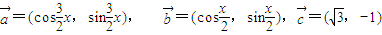
，其中x∈R，
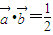时，求x值的集合；
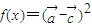，求f（x）的最小正周期及其单调增区间．
.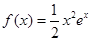