题目内容
已知函数f(x)=
sin(2x+ϕ),若f(a)=
,则f(a+
)与f(a+
)的大小关系是( )
| 3 |
| 3 |
| 5π |
| 6 |
| π |
| 12 |
A.f(a+
| B.f(a+
| ||||||||
C.f(a+
| D.大小与a、ϕ有关 |
由f(x)=
sin(2x+ϕ),且f(a)=
,得
f(a)=
sin(2a+φ)=
,
∴sin(2a+φ)=1,cos(2a+φ)=0.
由f(a+
)-f(a+
)
=
sin[2(a+
)+φ]-
sin[2(a+
)+φ]
=
sin[(2a+φ)+
]-
sin[(2a+φ)+
].
=
sin(2a+φ)cos
+
cos(2a+φ)sin
-
sin(2a+φ)cos
-
cos(2a+φ)sin
=
cos
-
cos
=
-
<0.
∴f(a+
)<f(a+
).
故选:B.
| 3 |
| 3 |
f(a)=
| 3 |
| 3 |
∴sin(2a+φ)=1,cos(2a+φ)=0.
由f(a+
| 5π |
| 6 |
| π |
| 12 |
=
| 3 |
| 5π |
| 6 |
| 3 |
| π |
| 12 |
=
| 3 |
| 5π |
| 3 |
| 3 |
| π |
| 6 |
=
| 3 |
| 5π |
| 3 |
| 3 |
| 5π |
| 3 |
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
=
| 3 |
| 5π |
| 3 |
| 3 |
| π |
| 6 |
=
| ||
| 2 |
| 3 |
| 2 |
∴f(a+
| 5π |
| 6 |
| π |
| 12 |
故选:B.

练习册系列答案
相关题目



 将
将 用“
用“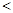 ”号连接起来为 .
”号连接起来为 .