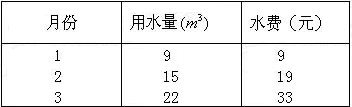
题目内容
我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的.某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定:
①若每月用水量不超过最低限量m立方米时,只付基本费9元和每户每月定额损耗费a元;
②若每月用水量超过m立方米时,除了付基本费和定额损耗费外,超过部分每立方米付n元的超额费;
③每户每月的定额损耗费a不超过5元.
(1)求每户每月水费y(元)与月用水量x(立方米)的函数关系;
(2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 4 | 17 |
| 二 | 5 | 23 |
| 三 | 2.5 | 11 |
分析:(1)根据水费=基本费+超额费+定额损耗费,把几项费用加到一起列出关于x的等式即得到.
(2)由于该家庭今年一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于最低限量m立方米.故可由(1)列出方程式求出x,y.再求出m,n,同理可以求出3月份的.即得到答案.
(2)由于该家庭今年一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于最低限量m立方米.故可由(1)列出方程式求出x,y.再求出m,n,同理可以求出3月份的.即得到答案.
解答:(1)解:依题意,得y=
其中0<a≤5.
(2)解:∵0<a≤5,
∴9<9+a≤14.
由于该家庭今年一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于
最低限量m立方米.
将
和
分别代入(**),
得
两式相减,得n=6.
代入17=9+n(4-m)+a,得a=6m-16.
又三月份用水量为2.5立方米,
若m<2.5,将
代入(**),得a=6m-13,
这与a=6m-16矛盾.(10分)
∴m≥2.5,即该家庭三月份用水量2.5立方米没有超最低限量.
将
代入(*),得11=9+a,
由
解得
故该家庭今年一、二月份用水超过最低限量,三月份用水没有超过最低限量,且m=3,n=6,a=2.
|
(2)解:∵0<a≤5,
∴9<9+a≤14.
由于该家庭今年一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于
最低限量m立方米.
将
|
|
得
|
两式相减,得n=6.
代入17=9+n(4-m)+a,得a=6m-16.
又三月份用水量为2.5立方米,
若m<2.5,将
|
这与a=6m-16矛盾.(10分)
∴m≥2.5,即该家庭三月份用水量2.5立方米没有超最低限量.
将
|
由
|
|
故该家庭今年一、二月份用水超过最低限量,三月份用水没有超过最低限量,且m=3,n=6,a=2.
点评:本小题主要考查函数和方程、分段函数等知识,考查函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用意识.

练习册系列答案
相关题目
(本题满分12分)
我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的。某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定:
①若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;
元;
②若每月用水量超过 立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付 元的超额费;
元的超额费;
③每户每月定额损耗费 不超过5元。
不超过5元。
(1) 求每户每月水费 (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2) 该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
|
月份 |
用水量(立方米) |
水费(元) |
|
一 |
4 |
17 |
|
二 |
5 |
23 |
|
三 |
2.5 |
11 |
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求 的值。
的值。
(本小题满分14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的.某市用水收费标准是:水费 基本费
基本费 超额费
超额费 定额损耗费,且有如下三条规定:①
若每月用水量不超过最低限量
定额损耗费,且有如下三条规定:①
若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;②
若每月用水量超过
元;②
若每月用水量超过 立方米时,除了付基本费和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费和定额损耗费外,超过部分每立方米付 元的超额费;③
每户每月的定额损耗费
元的超额费;③
每户每月的定额损耗费 不超过5元.
不超过5元.
(1) 求每户每月水费 (元)与月用水量
(元)与月用水量 (立方米)的函数关系;
(立方米)的函数关系;
(2) 该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
|
月份 |
用水量(立方米) |
水费(元) |
|
一 |
4 |
17 |
|
二 |
5 |
23 |
|
www..com 三 |
2.5 |
11 |
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求 的值.
的值.