题目内容
设集合A={x|x2-2x+2m+4=0},B={x|x<0}.若A∩B≠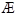 ,求实数m的取值范围.
,求实数m的取值范围.
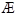 ,求实数m的取值范围.
,求实数m的取值范围.{m|m<-2}
(解法1)据题意知方程x2-2x+2m+4=0至少有一个负实数根.
设M={m|关于x的方程x2-2x+2m+4=0两根均为非负实数},
则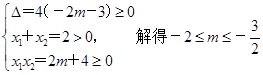
∴M=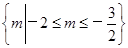 .
.
设全集U={m|Δ≥0}=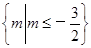 ,
,
∴m的取值范围是∁UM={m|m<-2}.
(解法2)方程的小根x=1-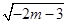 <0
<0
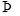
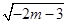 >1?-2m-3>1?m<-2.
>1?-2m-3>1?m<-2.
(解法3)设f(x)=x2-2x+4,这是开口向上的抛物线.因为其对称轴x=1>0,则据二次函数性质知命题又等价于f(0)<0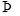 m<-2.
m<-2.
设M={m|关于x的方程x2-2x+2m+4=0两根均为非负实数},
则
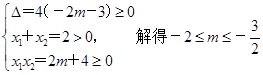
∴M=
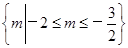 .
.设全集U={m|Δ≥0}=
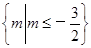 ,
,∴m的取值范围是∁UM={m|m<-2}.
(解法2)方程的小根x=1-
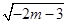 <0
<0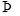
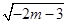 >1?-2m-3>1?m<-2.
>1?-2m-3>1?m<-2.(解法3)设f(x)=x2-2x+4,这是开口向上的抛物线.因为其对称轴x=1>0,则据二次函数性质知命题又等价于f(0)<0
 m<-2.
m<-2.
练习册系列答案
相关题目
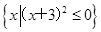 ,N={x|x2+x-6=0}.
,N={x|x2+x-6=0}.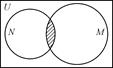
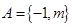 ,
,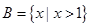 ,若
,若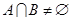 ,则实数
,则实数 的取值范围是 .
的取值范围是 .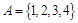 ,
,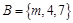 ,若
,若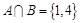 ,则
,则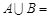 .
. ,则
,则 ( )
( ) 



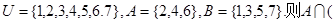
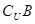 )=( )
)=( )