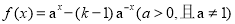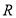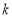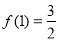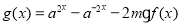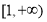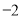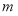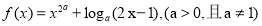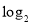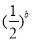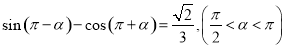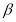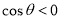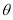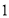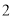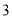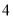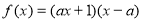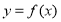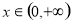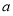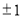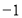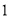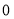题目内容
设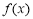 的定义域为
的定义域为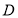 ,若
,若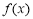 满足下面两个条件,则称
满足下面两个条件,则称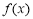 为闭函数.
为闭函数.
①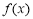 在
在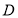 内是单调函数;②存在
内是单调函数;②存在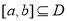 ,使
,使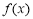 在
在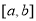 上的值域为
上的值域为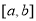 ,
,
如果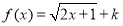 为闭函数,那么
为闭函数,那么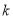 的取值范围是( )
的取值范围是( )
(A)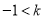 ≤
≤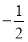 (B)
(B)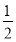 ≤
≤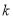 <1 (C)
<1 (C)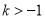 (D)
(D)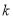 <1
<1
A
【解析】
试题分析:因为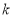 是常数,函数
是常数,函数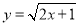 是定义在
是定义在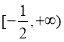 上的增函数
上的增函数
所以函数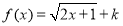 是
是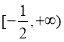 上的增函数,因此若函数
上的增函数,因此若函数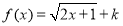 为闭函数,则可得函数
为闭函数,则可得函数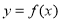 的图像与直线
的图像与直线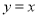 相交于点
相交于点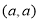 和
和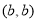 .如下图
.如下图
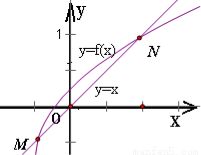
即 可得方程
可得方程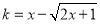 在
在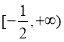 上有两个不相等的实数根
上有两个不相等的实数根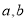 .
.
令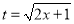 ,得
,得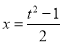 ,设函数
,设函数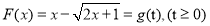
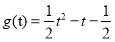 ,在
,在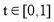 时,
时,  为减函数
为减函数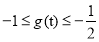 ;
;
在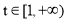 时,
时,  为增函数
为增函数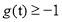 ;
;
所以当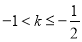 时,有两个不相等的实数
时,有两个不相等的实数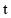 使
使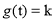 成立,
成立,
相应地有两个不相等的实数根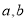 满足方程
满足方程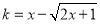
所以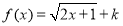 为闭函数时,实数k的取值范围是:
为闭函数时,实数k的取值范围是: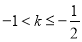 .
.
考点:函数单调性的性质;函数单调性的判断与证明.

练习册系列答案
相关题目