题目内容
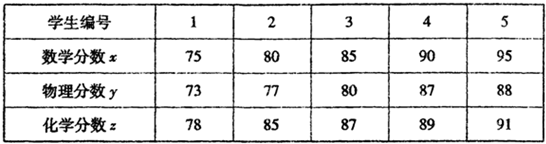
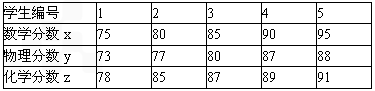
为了对某校高三(1)班9月调考成绩进行分析,在全班同学中随机抽出5位,他们的数学分数、物理分数、化学分数(均已折算为百分制)对应如下表:
(I)求这5位同学中数学和物理分数都不小于85分的概率;
(II)从散点图分析,y与x、x与x之间都有较好的线性相关关系,分别求y与x、z与x的线性回归方程,并用相关指数比较所求回归模型的拟合效果.
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 数学分数x | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 73 | 77 | 80 | 87 | 88 |
| 化学分数z | 78 | 85 | 87 | 89 | 91 |
(II)从散点图分析,y与x、x与x之间都有较好的线性相关关系,分别求y与x、z与x的线性回归方程,并用相关指数比较所求回归模型的拟合效果.
分析:(I)这5位同学中数学和物理分数都不小于85分,共有2人,故可得概率;
(II)根据最小二乘法计算可得回归方程中的b和a,回归直线方程即得,通过相关指数R2的计算可以得到回归方程的拟合程度.
(II)根据最小二乘法计算可得回归方程中的b和a,回归直线方程即得,通过相关指数R2的计算可以得到回归方程的拟合程度.
解答:解:(I)这5位同学中数学和物理分数都不小于85分,共有2人,故概率为P=
;
(II)设y与x、z与x的线性回归方程分别是?
=bx+a、
=b′x+a′,
根据所给的数据,可以计算出b=
=0.8,a=81-0.8×85=13,b′=
=0.6,a′=86-0.6×85=35.
∴
=0.8x+13、
=0.6x+35,
∴
(yi-
)2=02+02+(-1)2+22+(-1)2=6,
∴
(zi-
)2=(-2)2+22+12+02+(-1)2=10,
又y与x、z与x的相关指数是R2=1-
≈0.964、R′2=1-
≈0.90.
故回归模型
=0.8x+13比回归模型?
=0.6x+35的拟合的效果好.
| 2 |
| 5 |
(II)设y与x、z与x的线性回归方程分别是?
| ∧ |
| y |
| ∧ |
| z |
根据所给的数据,可以计算出b=
| 200 |
| 250 |
| 150 |
| 250 |
∴
| ∧ |
| y |
| ∧ |
| z |
∴
| 5 |
 |
| i=1 |
| ∧ |
| yi |
∴
| 5 |
 |
| i=1 |
| ∧ |
| zi |
又y与x、z与x的相关指数是R2=1-
| 6 |
| 166 |
| 10 |
| 100 |
故回归模型
| ∧ |
| y |
| ∧ |
| z |
点评:本题考查概率、相关系数的运算、回归直线方程的求法和回归模型的拟合效果判断等多方面知识和方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,
, 2=250,
2=250, ,
, ,
,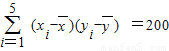 ,
, .
.