题目内容

下面有五个命题：
（1）函数y=sin⁴x-cos⁴x的最小正周期是π；
（2）终边在y轴上的角的集合是{a|a=

kπ

，k∈Z}；
（3）在同一坐标系中，函数y=sinx的图象和y=x的图象仅有一个公共点；
（4）把函数y=3sin（2x+

）的图象向右平移

个单位得到y=sin2x的图象；
（5）函数y=sin（

-x）在（0，π）上是增函数．
其中，真命题的编号是

（1）（3）

．（写出所有真命题的编号）

分析：函数y=sin⁴x-cos⁴x=sin²x-cos²x，=-cos2x，由此知函数y=sin⁴x-cos⁴x的最小正周期是π；终边在y轴上的角的集合是{a|a=kπ+

，k∈Z}；坐标系中，函数y=sinx的图象和y=x的图象仅有一个公共点；把函数y=3sin（2x+

）的图象向右平移

个单位得到y=3sin2x的图象；函数y=sin（

-x）=cosx在（0，π）上是减函数．

解答：解：∵函数y=sin⁴x-cos⁴x
=sin²x-cos²x
=-cos2x，
∴函数y=sin⁴x-cos⁴x的最小正周期是π，即（1）成立；
∵终边在y轴上的角的集合是{a|a=kπ+

，k∈Z}，即（2）不成立；
在同一坐标系中，函数y=sinx的图象和y=x的图象原点这一个公共点，
∵sinx=x只有一个解，
x＞0时，
sinx＜x；
x＜0时，
sinx＞x；
x=0时，
sinx=x．
故（3）成立；
把函数y=3sin（2x+

）的图象向右平移

个单位得到y=3sin2x的图象，故（4）不成立；
函数y=sin（

-x）=cosx在（0，π）上是减函数，故（5）不成立．
故答案为：（1），（3）．

点评：本题考查诱导公式的灵活运用，解题时要认真审题，仔细解答，注意三角函数的恒等变换．

练习册系列答案

寒假作业重庆出版社系列答案

下面有五个命题：
（1）函数y=sin⁴x-cos⁴x的最小正周期是π；
（2）终边在y轴上的角的集合是{a|a= $数学公式$ ，k∈Z}；　
（3）在同一坐标系中，函数y=sinx的图象和y=x的图象仅有一个公共点；
（4）把函数y=3sin（2x+ $数学公式$ ）的图象向右平移 $数学公式$ 个单位得到y=sin2x的图象；
（5）函数y=sin（ $数学公式$ -x）在（0，π）上是增函数．
其中，真命题的编号是________．（写出所有真命题的编号）

下面有五个命题：
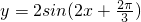（1）要得到 $数学公式$ 图象，需要将函数y=2sin2x图象向左平移 $数学公式$ 个单位；
（2）在△ABC中，表达式cos（B+C）+cosA为常数；
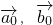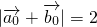（3）设 $数学公式$ 分别是单位向量，则 $数学公式$ ；
（4）y=cosx（0≤x≤2π）的图象和直线y=1围成一个封闭的平面图形，该图形的面积是2π．
其中真命题的序号是________（写出所有真命题的编号）