题目内容
设△ABC的内角A、B、C所对的边分别为a,b,c,若sinB+sinC=2sinA,3a=5c,则角B=( )
A. 60 B. 90
B. 90 C. 120
C. 120 D.150
D.150
C
解析试题分析:∵3a=5c,∴ 又∵sinB+sinC=2sinA,根据正弦定理可得b+c=2a,所以b+
又∵sinB+sinC=2sinA,根据正弦定理可得b+c=2a,所以b+ =2a,即
=2a,即 ,由余弦定理可得 cosB=
,由余弦定理可得 cosB= =
= =
=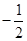 ,所以B= 120
,所以B= 120 ,故选C.
,故选C.
考点:正弦定理和余弦定理

练习册系列答案
相关题目
 的内角
的内角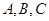 的对边分别为
的对边分别为 .若
.若 成等比数列,且
成等比数列,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
在 中,
中, 则
则 边上的高等于( )
边上的高等于( )
A. | B. | C. | D. |
在△ABC中,a=3,b= ,c=2,那么B等于( )
,c=2,那么B等于( )
| A.30° | B.45° | C.60° | D.120° |
在 中,
中, 分别为角
分别为角 的对边,若
的对边,若
 的面积为
的面积为 ,则
,则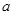 的值为( )
的值为( )
A. | B. | C. | D. |
在△ABC中,内角A,B,C的对边分别是a,b,c,若 ,
, ,则A=( ).
,则A=( ).
A. | B. | C. | D. |
已知△ABC中, =10,
=10, , A=45°,则B等于 ( )
, A=45°,则B等于 ( )
| A.60° | B.120° | C.30° | D.60°或120° |
 ,那么三边长a、b、c之间满足的关系是( )
,那么三边长a、b、c之间满足的关系是( ) B.
B. C.
C.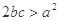 D.
D.