题目内容
(1)直线l过抛物线y2=2px(p>0)的焦点,且与抛物线相交于A(x1,y1),B(x2,y2)两点,证明:y1y2=-p2;
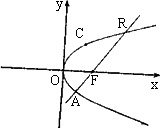
(2)直线l过抛物线y2=2px(p>0)的焦点,且与抛物线相交于A(x1,y1),B(x2,y2)两点,点C在抛物线的准线上,且BC∥x轴,证明:直线AC经过原点.
(2)直线l过抛物线y2=2px(p>0)的焦点,且与抛物线相交于A(x1,y1),B(x2,y2)两点,点C在抛物线的准线上,且BC∥x轴,证明:直线AC经过原点.
分析:(1)先设出直线方程(注意考虑斜率的存在性),再将直线与抛物线联立,运用韦达定理解决问题
(2)当斜率不存在时,直线x=
,此时A(
,p),B(
,-p),C(-
,-p),易证直线AC经过原点.当斜率存在,设直线方程为:y=k(x-
),与抛物线联立,运用韦达定理可求得k,进而证明直线AC经过原点
(2)当斜率不存在时,直线x=
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
解答:解(1)1°当斜率不存在时,直线x=
.此时A(
,p),B(
,-p),y1y2=-p2
2°当斜率存在,设直线方程为:y=k(x-
)
消元得:ky2-2py-kp2=0w所以 y1y2=-p2
综上所述y1y2=-p2
(2)1°当斜率不存在时,直线x=
,此时A(
,p),B(
,-p),C(-
,-p)
所以直线AC的斜率为kAC=
=2
所以直线AC的方程为y-p=2(x-
)⇒y=2x直线经过原点
2°当斜率存在,设直线方程为:y=k(x-
)
设A(
,y1),B(
,y2)C(-
,y2)
由
消元得:ky2-2py-kp2=0 y1y2=-p2;所以直线AC的斜率为kAC=
=
所以直线AC的方程:y-y1=
(x-
)⇒y=
x
所以直线经过原点.
综上所述,直线经过原点
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
2°当斜率存在,设直线方程为:y=k(x-
| p |
| 2 |
|
综上所述y1y2=-p2
(2)1°当斜率不存在时,直线x=
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
所以直线AC的斜率为kAC=
| -p-p | ||||
-
|
所以直线AC的方程为y-p=2(x-
| p |
| 2 |
2°当斜率存在,设直线方程为:y=k(x-
| p |
| 2 |
设A(
| y12 |
| 2p |
| y22 |
| 2p |
| p |
| 2 |
由
|
消元得:ky2-2py-kp2=0 y1y2=-p2;所以直线AC的斜率为kAC=
-
| ||||||
-
|
| 2p |
| y1 |
所以直线AC的方程:y-y1=
| 2p |
| y1 |
| ||
| 2p |
| 2p |
| y1 |
所以直线经过原点.
综上所述,直线经过原点
点评:本题考查了直线与抛物线的位置关系,特别是焦点弦的运用,解题时要充分利用抛物线的特殊性,灵活运用韦达定理解决问题

练习册系列答案
相关题目