题目内容
【题目】[选修4-1:几何证明选讲]
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.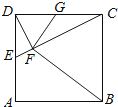
(1)证明:B,C,G,F四点共圆;
(2)若AB=1,E为DA的中点,求四边形BCGF的面积.
【答案】
(1)
证明:∵DF⊥CE,
∴Rt△DFC∽Rt△EDC,
∴ ![]() ,
,
∵DE=DG,CD=BC,
∴ ![]() ,
,
又∵∠GDF=∠DEF=∠BCF,
∴△GDF∽△BCF,
∴∠CFB=∠DFG,
∴∠GFB=∠GFC+∠CFB=∠GFC+∠DFG=∠DFC=90°,
∴∠GFB+∠GCB=180°,
∴B,C,G,F四点共圆.
(2)
∵E为AD中点,AB=1,∴DG=CG=DE= ![]() ,
,
∴在Rt△DFC中,GF= ![]() CD=GC,连接GB,Rt△BCG≌Rt△BFG,
CD=GC,连接GB,Rt△BCG≌Rt△BFG,
∴S四边形BCGF=2S△BCG=2× ![]() ×1×
×1× ![]() =
= ![]() .
.
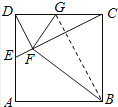
【解析】(1)证明B,C,G,F四点共圆可证明四边形BCGF对角互补,由已知条件可知∠BCD=90°,因此问题可转化为证明∠GFB=90°;(2)在Rt△DFC中,GF= ![]() CD=GC,因此可得△GFB≌△GCB,则S四边形BCGF=2S△BCG , 据此解答.;本题考查四点共圆的判断,主要根据对角互补进行判断,注意三角形相似和全等性质的应用.
CD=GC,因此可得△GFB≌△GCB,则S四边形BCGF=2S△BCG , 据此解答.;本题考查四点共圆的判断,主要根据对角互补进行判断,注意三角形相似和全等性质的应用.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目