题目内容
已知a=2-0.3,b=2-0.2,c=log
,那么a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 3 |
分析:根据指数函数的单调性比较a和b的大小,同时可断定a和b均小于1,运用对数函数的运算性质可得c大于1.
解答:解:因为a=2-0.3,b=2-0.2,由-0.3<-0.2,根据指数函数的单调性得:b>a.
b=2-0.2<20=1,而c=log
=log2-13-1=log23>1,
所以c>b>a.
故选A.
b=2-0.2<20=1,而c=log
| 1 |
| 2 |
| 1 |
| 3 |
所以c>b>a.
故选A.
点评:本题考查了对数值的大小比较,考查了指数函数和对数函数的性质,是基础题.

练习册系列答案
相关题目
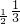 ,那么a,b,c的大小关系是
,那么a,b,c的大小关系是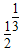 ,那么a,b,c的大小关系是( )
,那么a,b,c的大小关系是( ) ,那么a,b,c的大小关系是( )
,那么a,b,c的大小关系是( )