题目内容
(2010•宜春模拟)已知点P是双曲线
-
=1上的动点,F1,F2分别是其左、右焦点,O为坐标原点,则
的取值范围( )
| x2 |
| 8 |
| y2 |
| 4 |
| |PF1|+|PF2| |
| |OP| |
分析:设P(x,y) 则y2=
-4,e=
,由焦半径公式能够得出|PF1|=ex+a,|PF2|=ex-a,代入所求的式子并化简得到
,再由双曲线中x2≥8,求出范围即可.
| x2 |
| 2 |
| ||
| 2 |
| ||||||
|
解答: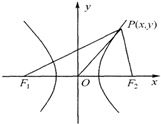 解:设P(x,y) 根据双曲线的对称性,不妨设x>0,
解:设P(x,y) 根据双曲线的对称性,不妨设x>0,
由焦半径公式|PF1|=ex+a,|PF2|=ex-a,
则
=
(y2=
-4,e=
),
则原式=
=
=
,又因为双曲线中x2≥8.
所以
∈(2,
].
所以
的取值范围为(2,
].
故选B.
 解:设P(x,y) 根据双曲线的对称性,不妨设x>0,
解:设P(x,y) 根据双曲线的对称性,不妨设x>0,由焦半径公式|PF1|=ex+a,|PF2|=ex-a,
则
| |PF1|+|PF2| |
| |OP| |
| ex+a+ex-a | ||
|
| x2 |
| 2 |
| ||
| 2 |
则原式=
| 2ex | ||||
|
| ||||
|
| ||||||
|
所以
| ||||||
|
| 6 |
所以
| |PF1|+|PF2| |
| |OP| |
| 6 |
故选B.
点评:本题考查了双曲线的性质、函数的值域等基础知识,考查运算求解能力,考查归与转化思想,属于中档题.

练习册系列答案
相关题目