题目内容
已知a,b,c分别为△ABC三个内角A,B,C的对边,a2=b2+c2﹣bc.
(Ⅰ)求A;
(Ⅱ)若a=2,求bsinB+csinC的最大值.
(Ⅰ)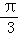 ;(Ⅱ)2
;(Ⅱ)2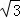
解析试题分析:(Ⅰ)利用余弦定理可解得cosA=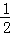 ,因此A=
,因此A=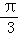 ;(Ⅱ)由正弦定理可知2r=
;(Ⅱ)由正弦定理可知2r=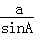 =
=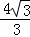 ,所以bsinB+csinC=
,所以bsinB+csinC=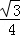 (b2+c2),又b2+c2﹣4=bc≤
(b2+c2),又b2+c2﹣4=bc≤ 得b2+c2≤8,所以bsinB+csinC=
得b2+c2≤8,所以bsinB+csinC=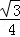 (b2+c2)≤2
(b2+c2)≤2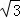 ,所求的最大值为2
,所求的最大值为2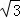 .
.
试题解析:(Ⅰ)△ABC中,∵a2=b2+c2﹣bc,∴cosA=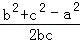 =
=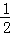 ,∴A=
,∴A=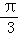 .
.
(Ⅱ)若a=2,则2r=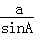 =
=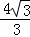 ,∴bsinB+csinC=
,∴bsinB+csinC=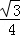 (b2+c2).
(b2+c2).
∵b2+c2﹣4=bc≤ ,∴b2+c2≤8,∴
,∴b2+c2≤8,∴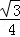 (b2+c2)≤2
(b2+c2)≤2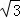 ,
,
即bsinB+csinC的最大值为2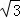 .
.
考点:1.正弦定理与余弦定理;2.基本不等式的应用

练习册系列答案
相关题目
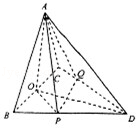
已知 ABC外接圆O的半径为1,且
ABC外接圆O的半径为1,且  ,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为
,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为 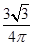 ,则
,则 MBC的形状为
MBC的形状为
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰直角三角形 |
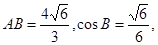 点D、E分别为AC、BC边的中点,且BD=
点D、E分别为AC、BC边的中点,且BD= ,
, 中,角
中,角 对的边分别为
对的边分别为 ,且
,且 .
. 的值;
的值; ,求
,求 .
. 为锐角,
为锐角, ,求
,求 的值.
的值. 中,
中, ,则角A =
,则角A =  中,
中, 分别为
分别为 的对边,若
的对边,若 ,且
,且 ,则角
,则角 ________
________ 分别是
分别是 的三个内角
的三个内角 所对的边,若
所对的边,若 且
且 是
是  与
与 的等差中项,则
的等差中项,则 =
=  中,
中, ,则
,则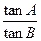 = 。
= 。