题目内容
三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,若PA=AC=| 2 |
分析:解题思路:“找球心”(到三棱锥四个顶点距离相等等的点).注意到PC是Rt△PAC和Rt△PBC的公共的斜边,记它的中点为O,从而得出该三棱锥的外接球球心为O,半径为1,从而计算出它的体积即可.
解答: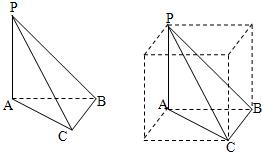 解析:∵到PC是Rt△PAC和Rt△PBC的公共的斜边,
解析:∵到PC是Rt△PAC和Rt△PBC的公共的斜边,
记它的中点为O,则OA=OB=OP=OC=
PC=1,即该三棱锥
的外接球球心为O,
半径为1,
故它的体积为:
π.
故答案为:
π.
 解析:∵到PC是Rt△PAC和Rt△PBC的公共的斜边,
解析:∵到PC是Rt△PAC和Rt△PBC的公共的斜边,记它的中点为O,则OA=OB=OP=OC=
| 1 |
| 2 |
的外接球球心为O,
半径为1,
故它的体积为:
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题主要考查线线垂直、线面平行、求球的体积等立体几何知识,以及分析问题与解决问题的能力.本题还有方法二:“补体”,将三棱锥补成长方体,如图所示;它的对角线PC是其外接球的直径,从而即可求得球的体积.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.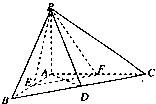 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,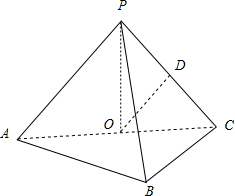 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.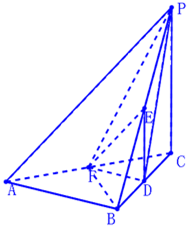 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.