题目内容
顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物 线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,…,过An(xn,yn)作抛物线的切线交x轴于B n+1(x n+1,0)
(1)求{xn},{yn}的通项公式;
(2)设an=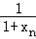 +
+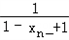 ,数列{an}的前n项和为Tn.求证:Tn>2n﹣
,数列{an}的前n项和为Tn.求证:Tn>2n﹣ .
.
(3)设bn=1﹣log2yn,若对任意正整数n,不等式(1+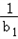 )(1+
)(1+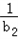 )…(1+
)…(1+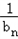 )≥a
)≥a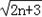 成立,求正数a的取值范围.
成立,求正数a的取值范围.
(1)求{xn},{yn}的通项公式;
(2)设an=
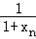 +
+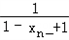 ,数列{an}的前n项和为Tn.求证:Tn>2n﹣
,数列{an}的前n项和为Tn.求证:Tn>2n﹣ .
.(3)设bn=1﹣log2yn,若对任意正整数n,不等式(1+
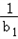 )(1+
)(1+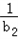 )…(1+
)…(1+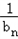 )≥a
)≥a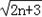 成立,求正数a的取值范围.
成立,求正数a的取值范围.
解:(1)由已知得抛物线方程为y=x2,y'=2x,
则设过点An(xn,yn)的切线为y﹣xn2=2xn(x﹣xn),
令y=0,x= ,故x n﹣1=
,故x n﹣1= ,
,
又x0=1,∴xn=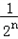 ,yn=
,yn= ,
,
(2)证明:由(1)知xn= ,
,
所以an= +
+ =
= +
+ =2﹣(
=2﹣( ﹣
﹣ ),
),
由于 <
< ,
, >
> ,
,
得 ﹣
﹣ <
< ﹣
﹣ ,
,
∴an=2﹣( ﹣
﹣ )>2﹣(
)>2﹣( ﹣
﹣ ),
),
从而Tn=a1+a2+a3+…+an>2n﹣[( ﹣
﹣ )+(
)+( ﹣
﹣ )+…+(
)+…+( ﹣
﹣ )]
)]
=2n﹣(
 )>2n﹣
)>2n﹣ ,
,
即Tn>2n﹣ ,
,
(3)由于yn= ,故bn=2n+1,对于任意正整数n,
,故bn=2n+1,对于任意正整数n,
不等式(1+ )(1+
)(1+ )…(1+
)…(1+ )≥a
)≥a ,
,
a≤ (1+
(1+ )(1+
)(1+ )…(1+
)…(1+ )恒成立,
)恒成立,
设f(n)= (1+
(1+ )(1+
)(1+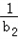 )…(1+
)…(1+ ),
),
∴f(n+1)= (1+
(1+ )(1+
)(1+ )…(1+
)…(1+ )(1+
)(1+ ),
), =
= ×(1+
×(1+ )=
)=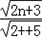 ×
× =
= =
= >1,
>1,
∴f(n+1)>f(n),故f(n)为递增,
∴f(n)min=f(1)= ×
× =
= ,
,
∴0<a≤ .
.

练习册系列答案
相关题目
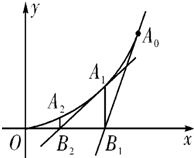 顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物 线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,…,过An(xn,yn)作抛物线的切线交x轴于Bn+1(xn+1,0)
顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物 线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,…,过An(xn,yn)作抛物线的切线交x轴于Bn+1(xn+1,0)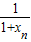 +
+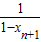 ,数列{an}的前n项和为Tn.求证:Tn>2n-
,数列{an}的前n项和为Tn.求证:Tn>2n- .
.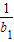 )(1+
)(1+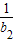 )…(1+
)…(1+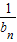 )≥a
)≥a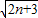 成立,求正数a的取值范围.
成立,求正数a的取值范围.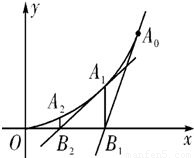
 +
+ ,数列{an}的前n项和为Tn.求证:Tn>2n-
,数列{an}的前n项和为Tn.求证:Tn>2n- .
. )(1+
)(1+ )…(1+
)…(1+ )≥a
)≥a 成立,求正数a的取值范围.
成立,求正数a的取值范围.
 ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 .
.
 ;
; ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
; ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式 …
… ≥
≥ 成立,求正数a的取值范围.
成立,求正数a的取值范围. ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 .
. ;
; ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
; ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式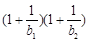 …
… ≥
≥ 成立,求正数a的取值范围.
成立,求正数a的取值范围.