题目内容
已知向量 、
、 不共线,若
不共线,若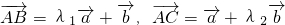 ,且A、B、C三点共线,则关于实数λ1、λ2一定成立的关系式为
,且A、B、C三点共线,则关于实数λ1、λ2一定成立的关系式为
- A.λ1=λ2=1
- B.λ1=λ2=-1
- C.λ1λ2=1
- D.λ1+λ2=1
C
分析:先求A、B、C三点共线的充要条件,我们要先根据已知条件a、b是不共线的向量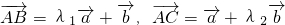 ,判断λ与μ满足的关系;并以此关系为已知条件,看能不能反推回来得到A、B、C三点共线.如果两个过程都是可以的,该关系式即为所求.
,判断λ与μ满足的关系;并以此关系为已知条件,看能不能反推回来得到A、B、C三点共线.如果两个过程都是可以的,该关系式即为所求.
解答:由于 ,
, 有公共点A,
有公共点A,
∴若A、B、C三点共线
则 与
与  共线
共线
即存在一个实数t,使 =t
=t 
即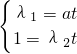
消去参数t得:λ1λ2=1;
反之,当λ1λ2=1时
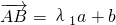
此时存在实数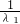 使
使  =
=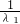

故 与
与  共线
共线
又由 ,
, 有公共点A,
有公共点A,
∴A、B、C三点共线
故A、B、C三点共线的充要条件是λ1λ2=1.
故选C.
点评:判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
分析:先求A、B、C三点共线的充要条件,我们要先根据已知条件a、b是不共线的向量
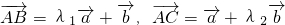 ,判断λ与μ满足的关系;并以此关系为已知条件,看能不能反推回来得到A、B、C三点共线.如果两个过程都是可以的,该关系式即为所求.
,判断λ与μ满足的关系;并以此关系为已知条件,看能不能反推回来得到A、B、C三点共线.如果两个过程都是可以的,该关系式即为所求.解答:由于
 ,
, 有公共点A,
有公共点A,∴若A、B、C三点共线
则
 与
与  共线
共线即存在一个实数t,使
 =t
=t 
即
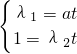
消去参数t得:λ1λ2=1;
反之,当λ1λ2=1时
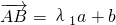
此时存在实数
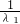 使
使  =
=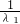

故
 与
与  共线
共线又由
 ,
, 有公共点A,
有公共点A,∴A、B、C三点共线
故A、B、C三点共线的充要条件是λ1λ2=1.
故选C.
点评:判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
 =k
=k =2
=2

 、
、 不共线,
不共线, =k
=k -
- ,
, =2
=2 +
+ ,若
,若 ∥
∥ ,则实数k的值为( )
,则实数k的值为( )

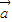 、
、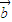 不共线,若
不共线,若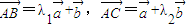 ,且A、B、C三点共线,则关于实数λ1、λ2一定成立的关系式为( )
,且A、B、C三点共线,则关于实数λ1、λ2一定成立的关系式为( )