题目内容
若函数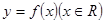 满足
满足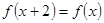 ,且
,且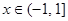 时,
时,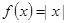 ,则函数
,则函数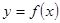 的图象与函数
的图象与函数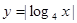 图象的交点个数为__________。
图象的交点个数为__________。
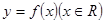 满足
满足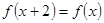 ,且
,且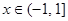 时,
时,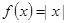 ,则函数
,则函数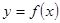 的图象与函数
的图象与函数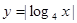 图象的交点个数为__________。
图象的交点个数为__________。4
试题分析:根据题意,由于函数
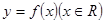 满足
满足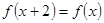 ,周期为2,且
,周期为2,且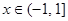 时,
时,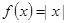 ,则函数
,则函数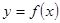 的图象与函数
的图象与函数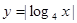 图象的交点个数为通过作图可知当x
图象的交点个数为通过作图可知当x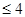 时,则可知有交点,那么交点的个数为4个,故答案为4.
时,则可知有交点,那么交点的个数为4个,故答案为4.点评:主要是考查了函数图象的交点问题的运用属于中档题。

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
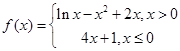 的零点个数是 .
的零点个数是 .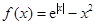 的图象是 ( )
的图象是 ( )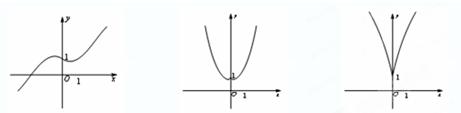
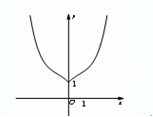
 ,则函数
,则函数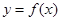 的极大值点为( )
的极大值点为( )



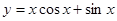 的图象大致为( )
的图象大致为( )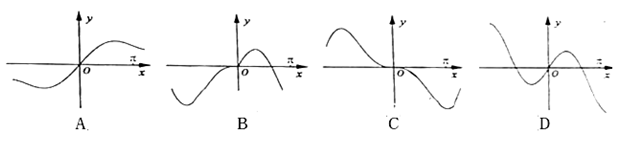
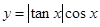 的部分图象是( )
的部分图象是( )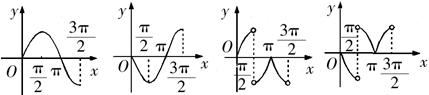
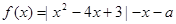 恰有三个不同的零点,则实数a的值是( )
恰有三个不同的零点,则实数a的值是( )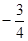
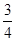
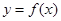 (
(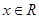 ),满足:
),满足: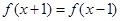 ,且
,且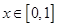 时,
时,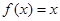 ,则函数
,则函数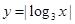 图像的交点个数为 .
图像的交点个数为 . 是函数
是函数 图像上的点,
图像上的点, 是函数
是函数 图像上的点,且
图像上的点,且 两点之间的距离
两点之间的距离 能取到最小值
能取到最小值 ,那么将
,那么将 和
和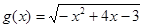 之间的距离是 .
之间的距离是 .